圖源：Pixabay

撰文 | 丁玖

● ● ●

最近在《知識分子》上讀到一篇特寫《數學戰爭警示錄：我們需要什麼樣的數學教育？》，頗有感觸。在這俄烏戰爭已持續三年有餘、中東衝突也不時陰雲密佈的不安全世界中，文章標題前半部中的“戰爭”一詞，確實容易觸動讀者那敏感的厭戰神經，儘管它比喻的是由於美國教育家和數學家關於“數學教育”長期論戰累積而成的瀰漫在北美上空的“戰爭煙火”。這一場曠日持久的“數學戰爭”的直接遭殃者是美國的一代代學生。標題下半部的問話——“我們需要什麼樣的數學教育？”，倒是一個好問題，因爲它對中美兩國師生都是至關重要的大問題。

可是，這又是一個極難回答的問題。如果數學教育家、職業數學家、中小學數學老師、修數學課的青少年學生和學生家長各任命幾位代表組成“評分委員會”的話，那麼他們對此的討論將會異常激烈。

無論在美國還是在中國，這幾類人對“數學教育”的釋義、理解及觀念可能彼此大相徑庭，提出的求解思路甚至可能南轅北轍。然而，集思廣益、暢所欲言，先觀察、後思索、想出路、提方案，總是解決棘手問題的一個良策。所以我們作爲《知識分子》的忠實讀者，應該積極應對，想方設法，從他國的正反實踐中吸取教訓，共同努力提高我國數學教育的水平和效率。

今年六月一日，我從教了整整三十五年書的一所美國研究型公立大學正式退休，積累了對這個國家從初等到高等數學教育方方面面的若干觀察。在這篇文章裏，我試圖描述我所看到乃至親身體驗的美國數學教育，並提出自己的點滴感想，以拋磚引玉。

14-5等於11？

我於1986年元旦赴美，去了密歇根州立大學數學系讀博士學位。爲了獲得工作報酬支付讀書及生活開銷，我同時也在系裏擔任教學助理，先當習題課老師，後主講小班初等微積分。1990年獲得學位後，我應聘擔任另一所州立大學的正式助理教授而開始全職教書，直至退休。

之前，我在國內也教過數學，最早的實踐是在14週歲那年，剛高中畢業不久的我當了一個月的代課老師，教了一個初中班的數學，第一節課講的是怎樣計算球冠的體積。1984年在本科母校南京大學數學系拿到碩士學位後，我留系任教，第一個學年教了物理系和天文系新生的基礎課“甲類高等數學”，第二個學年的秋季學期教了本系大四學生的專業課“最優化理論和方法”，然後我就出國留學去了。在過去的幾十年間，利用回國訪問的機會，我也曾在多地多次講授過大學數學課程。這樣說來，我在中美兩國都教過書，對兩國的教育尤其是數學教育有進行一些比較的基礎。

我對美國數學教育的初步印象產生在我到達留學目的地密歇根州立大學後的第一個學季中，2016年，商務印書館出版了我的書《親歷美國教育：三十年的體驗與思考》，書中第三章專門回憶了我這個新來乍到的外國研究生“新的發現”，包括對美國理工科大學生數學知識現狀的發現：

“來到佔地面積可以覆蓋五十個南大鼓樓老校區的密歇根州立大學，第一次給美國大學生教室答疑前，我想，班上是全世界最發達國家的學生，他們的腦子也一定是最靈光的，知識也一定是最豐富的，一定要使出渾身解數教，不能讓他們小看自己。沒想到，一個小時下來，學生問的問題十分簡單，都是我想都不要想就能完全回答的。比如像多項式這樣的最簡單初等函數的導數運算，或一元二次方程的求根公式。我驚訝地發現，大部分人都背不出我們從小就記得滾瓜爛熟的最基本代數恆等式，像平方差公式之類的。我甚至都懷疑他們是否讀過高中，因爲這些初等代數的知識對於中國的大部分初中生，都已掌握得透熟。這樣的學生畢業後，真的能成爲美國各行各業到處都有的傑出科學家和工程師嗎？剛剛進入美國高等教育體系的我，真是百思不得其解。”

我當時的日記中還記下了另一件事。那天是1986年10月9日，我因監考所教習題課班級的期中考試而在教室內來回走動，無意中瞟見一名女生在答卷上將14-5的答案寫成等於11，目睹此等中國小學一年級水平的算術錯誤，我心生憐憫之心，便用手指了一指這個“等式”暗示她再好好地算一下，但她卻堅持回答我：“Yes, it’s eleven（對，就是11）”。我於是無計可施，舉手投降。

剛到美國不久的我，由於在教學中常碰到這類例子，開始尋找“爲何是這樣？”的答案。我曾經猜測，原因或許是這個有四萬五千名學生的大學規模太大，或者是由於基礎課大班超過百人的聽課學生人數太多，從而使得講課教授的教學效果不彰。其實不然，十年後我的一位朋友告訴我，他所任教的美國一所著名的私立人文學院，雖然全校只有區區兩千多名學生，而且從全國各地考進去的基本上都是高中母校的優秀畢業生，但班上的大學生，絕大多數根本沒背過解一元二次方程的求根公式。然而，這個學校的畢業生中卻出了無數個傑出人才，包括了宋美齡、謝冰心、希拉里·克林頓(Hillary R. Clinton) 和瑪德琳·奧爾布賴特(Madeleine Albright)等中國人耳熟能詳的鼎鼎大名。又過了十來年，我的教授朋友請我去給他班上的學生講點“函數迭代”的基本思想，在我準備講稿時他關照我“講淺點，講淺點”。

我就讀的密歇根州立大學是一所很不錯的公立大學，它是美國第一家“政府授地”大學，也是第一家農學院，理工科各系都有成就斐然的學者，有不少專業在全美享有盛名，包括排名第一的核物理。照理說，新生們在高中階段應該學得很好，尤其是進理工院系深造的那些，應該已經將高中數學——代數、幾何、三角——透徹地掌握了。然而現實卻打破我的想象，我決定要在接下來的日子裏繼續觀察。

02

數學教育家和數學家之戰

我發現其中一個根源是美國那羣“數學教育家”，這些數學教育領域的專家或行政官員，他們中一般從事教育方法的教學和研究，但對教育的學科內容卻關注不夠，甚至缺乏有足夠深度的理解。他們中的大部分在教育學院任教。他們的教育理念經過幾代人的繼承和推進已經根深蒂固，連那些深諳教育之道並且熱愛學生的著名創造型數學家也難以撼動。

這種理念在美國大概發端於百年前實用主義哲學家杜威的現代教育學說，更早的源頭可在十九世紀法國啓蒙主義思想家的部分著作中找到。可是，正如列寧說過的一句告誡之語“真理哪怕是向前邁出一小步就會變成謬誤”，正是那些不懂教育真諦卻能決定教育方式的那些人，誤將啓蒙主義的思潮用於自身具有特殊規律的教育領域而導致了美國數學教育的大潰敗。

幾十年間，美國推崇“進步主義(progressivism)”哲學與持傳統教學觀念的兩派數學工作者，彼此之間因觀念衝突而持續較量，結果是廣大民衆對中小學數學教育不斷下降的水平日趨不滿。在此大背景下，已打下進步主義烙印的國家數學教師委員會於1980年提出了一個標題爲“行動的規則”(An Agenda for Action)的報告，其中稱基礎數學教育要“立足於解決問題”，而不能“先完全掌握解題技能”，主張甚至小學生也應被允許用計算器而不是用手算。報告強調學生“探索式發現”以解決真實世界的問題。這樣一來，高中傳統數學課程可以不分代數幾何三角分門別類講授，而是一鍋端，形成十年後的“綜合數學”大雜燴課本，甚至日後微積分的重要性也被弱化。

到了1989年，國家數學教師委員會進一步提出了“學校數學課程和測試標準”，它的24名制定者除了兩位是中小學教師外，其餘大都是教育學院的教授，數學家的數目爲零。然而，這種數學內容不夠的“標準”爲何能在全美大行其道呢？一個原因是進步主義教育專家們善於玩弄概念遊戲來蠱惑人心，比如誤導性採用“認知心理學”中的建構主義(constructivism)來宣傳他們所提倡的教育理念。

一些在學術研究之外願意花時間的數學家特此撰文批駁。《美國數學會通告》也刊登過一些著名數學家的文章，重鋪數學教育的“正確之道”。二十年前，我在美國數學會的一次地區性會議的數學教育分會場，親眼目睹華裔數學家伍鴻熙教授舌戰一羣數學教育家，批評他們撰寫的中小學數學教材“不合邏輯”。正因爲無意中發現加州公立學校的數學教育狀況令人憂慮，這位幾何學家挺身而出，爲全美數學教育走向正常化奮鬥到正式退休爲止。

到了九十年代初，我已經成了一名助理教授，美國國家科學基金會也加入了“進步主義”的行列，除了大力打造中小學數學教材，也對大學的微積分教科書開始“改革”，其中最著名的當數所謂的“哈佛微積分”。這本教材的掛帥編者是哈佛一名教育學院的教師，編寫組人員爲其他參與大學和中學的幾位老師，包括我係的一對夫婦，丈夫是早已不做數學研究的資深副教授，太太是隻有碩士學位的講師。由於他們進入了寫作班子，作品出爐後我係必須用它作爲微積分教本。這不僅令任課教師苦惱，更讓修課學生糊塗，因爲此書到處都是計算器的影子，學生只能盲目跟着它們去“探索發現”微積分的奧祕。對等地，通常對微積分的先修課程高中代數的要求降到了最低。

圖源：Pixabay

作爲一個例子，我們看看這本書是怎樣講授函數的導數的。這是微積分裏學完連續函數後的第一個關鍵概念，是積分思想的前奏曲。然而，本書讓首次學到這個新概念的大一新生如同在修一門計算數學專業課：用差商代替導數！這就是進步主義者奉若神明的“探索性學習法”，什麼極限過程，什麼“ε-δ”語言，統統滾蛋!這本教材似乎要讓學生相信：導數就是差商，只要對自變量取非常靠近的兩個數，求出它們對應的函數值，然後做兩個減法，在將它們相除一下，導數就現身而出。

在國家數學教師委員會那個臭名昭著1980年報告問世三年後，幸好里根總統政府教育部任命的一個特設委員會提出了一個觀點針鋒相對、目標截然不同的報告《危險中的國家》(A Nation at Risk)。它並非聳人聽聞地指出：“我們國家的教育基礎正被平庸所侵蝕，威脅着我們國家和民族的未來”。它悲哀地發現，未來充實數學教師隊伍的大學新生，許多人基礎薄弱，在高中成績位於中下到墊底不等。這樣的人未來手執教鞭，豈不誤人子弟？然而，重病在身的美國數學教育，四十年來卻未能恢復元氣，至今仍未康復。

美國普通數學教育失敗在哪裏

跨入新世紀，我也在大學全職教了十年書，講授了多門或淺或深從本科到博士不等的數學課，從高中生學過的初等代數到博士生基礎課泛函分析我都教過。儘管我的教學受到學生們普遍的讚揚，連我的教授同事也說我“是個天生的教師”，然而在教書這一點上，我內心一直感到悲哀：班上絕大多數學生包括研究生的數學認知程度是差之又差的，他們無法與我教過一年半的南京大學的學生比。當然，這在美國幾乎所有的公立大學都是一般性的存在。

既然國家層面早就認識到提升中小學生數學知識的戰略重要性，爲什麼美國普通大學生的數學水平幾十年來難以提高？冰凍三尺非一日之寒。這一方面來自上節所述的關於教育措施的兩派觀念之爭，另一方面，這也與長期以來美國中小學數學教師的素質有關。

我曾經多次教過本系夏季學期研究生課程，班上的學生除了碩士生或博士生外，還有部分是隻能在暑假前來註冊修課的高中數學老師，有的甚至來自外州，他們在職攻讀數學教育碩士或博士學位。十餘年前，爲了讓這些中學數學老師學到一點現代數學分支離散動力系統的概念和方法，我開了一門名叫“動力幾何”的課，意在通過迭代三角形，讓學過甚至教過歐幾里得平面幾何的他們開啓從有序到混沌的幾何之旅。

當講到“垂足三角形”迭代並構造其對應的一類我曾參與研究並發表過幾篇學術論文的分形時，我先在黑板上畫上一個銳角三角形，然後從它的每一個頂點作其對邊的垂線，得到的三個垂足構成原先三角形的垂足三角形，將這個三角形拿走（三條邊保留下來），那麼原先的大三角形內剩下三個小三角形，這完成了製造對應分形的無窮次迭代的第一次迭代，之後對每一個剩下的更小三角形如法炮製，直至無窮。爲了獲得最終形成的那個稱之爲“謝爾賓斯基垂足三角形(Sierpiński pedal triangle)”分形的維數性質，需要證明這三個小三角形都與初始選定的大三角形相似。見下圖所示：

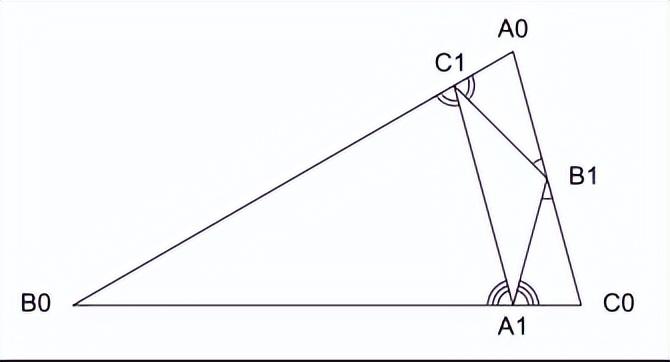
要證明這大小四個三角形兩兩相似，即證明它們的對應角相等，只需用到三垂線交於一點的事實和四點共圓及圓周角的性質，這些都是初等幾何的基本內容。我相信中國讀過中學數學的人都應該會做，考上大學的更不在話下了。既然聽我課的都是研究生和中學數學教師，我想請他們來證明，順便摸摸他們的數學根底，於是我就問誰願意上黑板展示一下。我等了很久，卻沒有一個人舉手上講臺。

這就是美國中學數學老師自我畫出的一幅數學圖景。他們在本國接受了全部的教育，在小學階段基本上是不被要求熟記“小九九乘法口訣表”的，因爲他們的老師和家長也沒有背過，然而他們很早就學會使用電子計算器，因爲有影響力的教育專家們鼓勵他們只管用，而計算器製造商則依賴有天賦和創造力的工程師不斷革新產品，不停增強計算畫圖功能，讓這幫孩子用得方方便便，愛不釋手，答案手到擒來。

在中學階段，他們的老師解一元一次方程時在黑板上分五步做，比方說解3x + 2 = 5。第一步，兩邊加上-2：3x + 2 + (-2) = 5 + (-2)；第二步，改寫：3x + 0 = 3；第三步，化簡：3x = 3；第四步，兩邊除以3：3x/3 = 3/3；第五步，化簡得到解：x = 1。老師這樣教是因爲他們不知道“移項換符號”的便利，也沒有人曾讓他們像中國初中生那樣可以一步到位快速完成這些簡單運算並一口清地報告答案。更不用說在初中代數課堂上，老師會命令學生背誦平方差公式等最基本的代數恆等式。

到了高中學平面幾何，看上去厚厚的教材印刷精美，圖形五彩繽紛，文字引人入勝。然而卻少了中國幾何教本中的最重要內涵：推理證明。在“探索法學習”的大旗指引下，學生捧在手中的幾何讀本，功能幾乎等同於“直觀理解”，似乎在“看圖識字”，而拋棄了歐幾里得幾何的精髓。這個精髓就是：通過寥寥幾條公理和公設，推演出平面幾何的所有命題，如三角形的內角和必定是180度。這個精髓引領了近代科學，把人類從愚昧中解救了出來。

這就能解釋爲何我講授《高等微積分》學年課程第一學期的期中考試第一題，絕大多數修課的數學系本科生和研究生都做不出來，因爲他們在高中沒有受過幾何證明的洗禮。而這些答不出試卷本科生中的相當一部分人將來的職業是中學數學老師。這道題是關於一個數集的上確界和下確界，該簡單數集由所有分數1/n - 1/m組成，其中n和m取所有的自然數。儘管我早已清楚現實的殘酷，講授確界概念時花了遠超教學大綱中計劃的時間，翻來覆去地舉例解釋上確界的定義，闡述其意思：它是給定數集的一個上界，且在該數集的所有上界中，它最小，即它是數集的“最小上界”。我也用ε-語言刻畫了上確界：數s爲數集A的上確界，當且僅當s大於或等於A中的所有數，且對任意正數ε，存在A中的數a使得a > s - ε。這個不等式給出“比上確界更小的數不是上界”的數學表達。

自然，精確理解這些等價語言，必須具有邏輯推理的足夠武功，而這套武功的最初練武場就是中學平面幾何命題證明的課堂——這個練武場在美國的普通高中不知蹤影。

截然不同的精英教育

但是，上述事例並不能得出美國的數學教育一塌糊塗的結論，更不能用來否定美國各地對資優教育的極端重視。美國的教育方式和它的意識形態具有相當的一致性，大體上是“崇尚自由”。在學校，教師對學生的數學學習是除了必修課外，“任君取捨”，但對母語的訓練不遺餘力，因而進入大學的學生，數學可以將1/2 + 1/3算成2/5，但幾乎個個能說會道，絕不害羞。另一方面，每所普通高中都有小部分高天賦學生，他們也有鴻鵠之志，對這樣的好學生，學校給他們開小竈，或修大學先行課程如“AP微積分”，或送到附近的大學修課。因此美國青少年中的前百分之幾的聰明好學者，最終成長爲改變美國甚至改變世界的領路人。

多年的觀察讓我早就看到，雖然美國普通理工科大學生的數學基礎，和中國的同類大學生比起來弱得多，但是在諸如斯坦福大學就讀的精英大學生中，許多人的數學本領強於中國名牌大學的數學尖子。但在本文，我們不討論資優教育，僅僅着眼於從美國對普通學子數學教育的“失算”歷史回顧中吸取怎樣的教訓。

我們需要什麼樣的數學教育

如上對美國中小學數學教育所走彎路以及對大學數學教育造成危害的簡要描述，實際上給我們回答《知識分子》的提問“我們需要什麼樣的數學教育？”提供了一點線索，那就是：好的數學教育應該是好的老師有效傳授給學生對未來的發展行之有效的基礎知識、基本技能，培養創造性思維的能力和舉一反三應用所學的功夫。

更具體地說：人類千百年間發現的數學基礎知識是前人留下的寶貴財產，是後人能夠創新的雄厚資本。青少年階段應該像海綿般地沉浸於此，爲未來打下堅實的基礎。熟練操作的基本技能是牢固掌握基礎知識以便將來能熟練應用所學知識的關鍵，容不得有半點的虛假和討巧。只有在全面吸收基礎知識以及對基本技能運用自如後，人們纔有能力和潛質進一步從事“探索式的學習”，進入更高層次的學習，乃至走向創造新知識、發明新技術之路，而不是過程相反，在缺乏基礎知識和基本技能的情形下，就能輕而易舉地發現新知識。這就是數學教育的邏輯所在和基本規律。那種打着“探索性自主式學習”旗號的“進步主義教學法”

，教出的學生只能是知識結構殘缺不全卻容易好高騖遠，因爲他們本來就空空的腦袋不可能容易無中生有地探索出未曾學過的知識來。