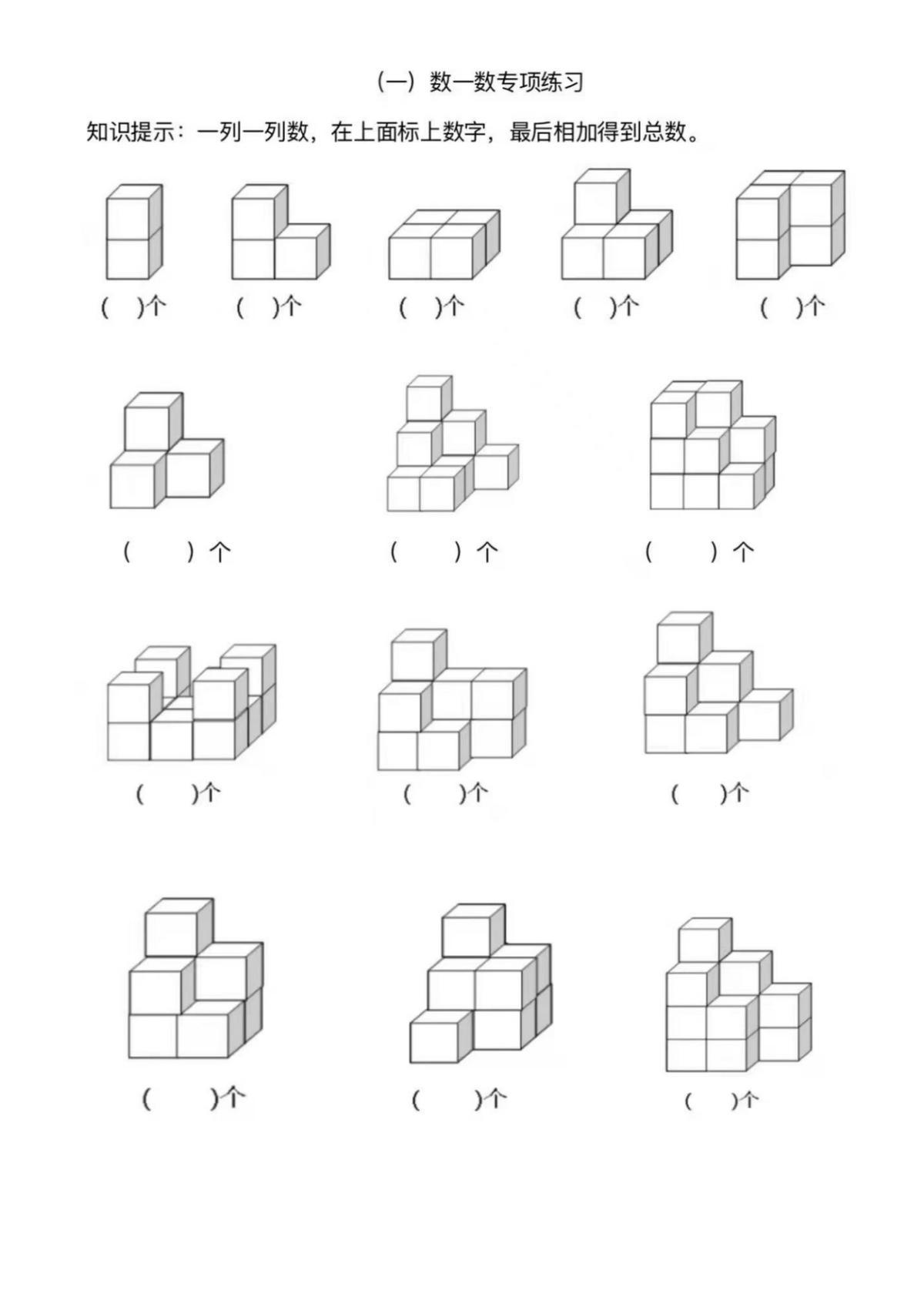
一年級數學：立方體圖形計數，這樣做正確率很高，還很快

理科女一枚，對數學有着迷之熱愛~

果媽 · 書

你好呀，我是果媽~

在果媽小學的時候，數學可沒有數小立方體塊數這類題目。

然而，現在這種題目，竟然出現在一年級的數學題中，這也不知道是在爲難誰。

不過，果媽發現，在研究解題思路之後卻發現：這種題目，真的很適合一年級孩子啊！這就是妥妥的立體思維題。

傳統思維

按照傳統思維，這種題目，就是一個一個立方體地數。

但是，非常容易數錯，畢竟，有些立方體被隱藏在底下，如何能數？

所以，按照傳統一個一個數的方法，層數矮、個數少的，不容易出錯，但是，一旦層數高一些，被遮擋的立方體多一些，孩子就很容易出錯了。

別說孩子，果媽在沒找到“巧解”的時候，也是這麼做的，也容易出錯。

所以，這種題目，考驗的不僅僅是孩子的空間感、立體思維，更是考驗了孩子的思維能力。

又或者，有些家長會拿出立方體地教具，搭出和題目一樣的立方體形狀，然後一個個數。

這樣的方式，雖然不容易出錯，但是，不可能每次做題都這麼擺一下。這種方法，僅可用在孩子剛接觸這種題，理解做法的時候。

立方體圖形計數“巧思”

立方體圖形計數，可不能一個一個數，是有“巧思”的，而且，還有2種方法。

這兩種方法，孩子都掌握了，不僅可以快速解題，還能夠在用完第一個方法得到答案之後，再用第二種方法，去驗證答案是否正確。

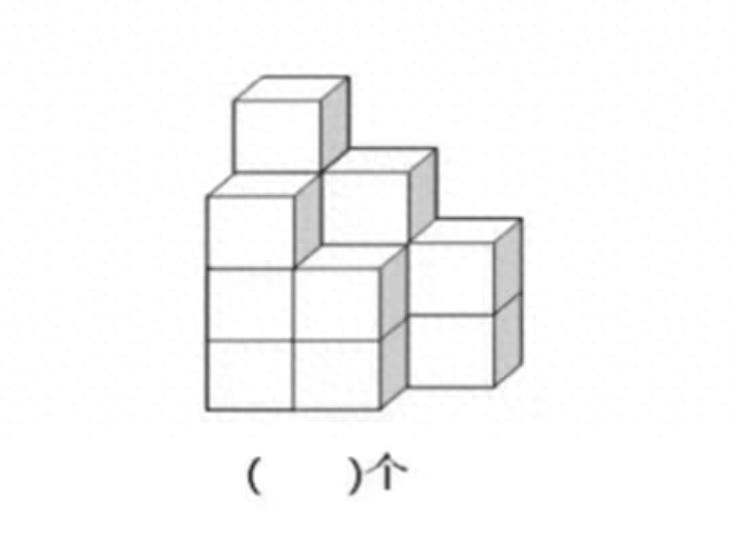
就以這道題目爲例。

方法一：按列計算

按列算，就是數每一列立方體的數，但是不需要一個一個數，只需要數“最頂上”一個就可以。

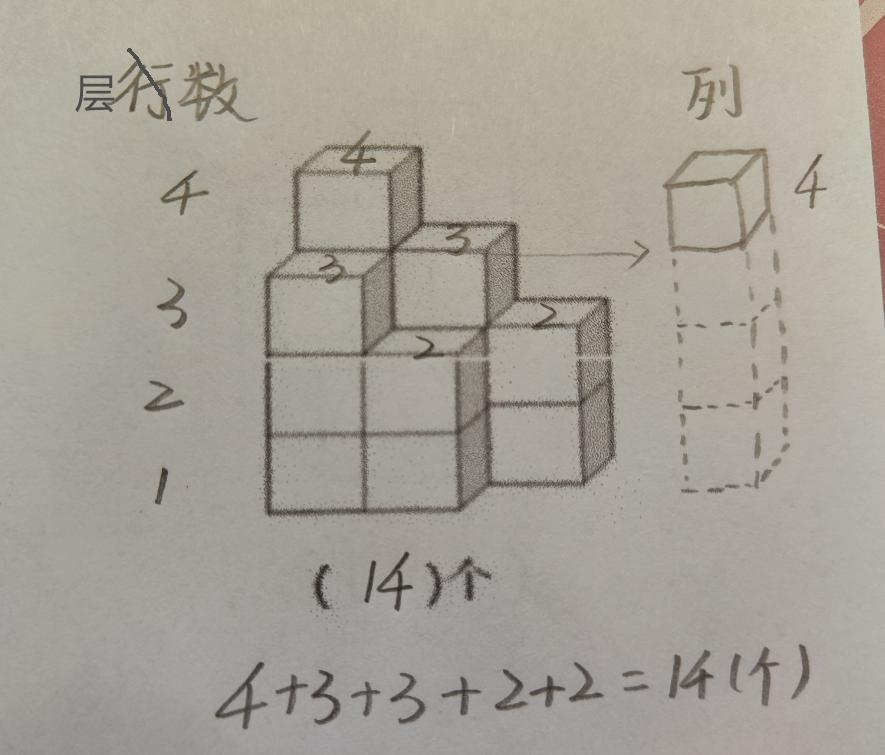
能夠看到小立方體頂面的，在第幾層，就在小立方體上標記幾，代表這一列有幾個正方體。

就比如，這邊的第4層，只有一個能夠看到頂面的立方體，那就標記4。

爲什麼這一列是4個？

可以看右側的分解圖，可以看出，這個能夠看得到的立方體，在第四層，然後看不到的地方，還有3個立方體，在下面的3層，支撐着這最頂上的立方體。

所以，第4層能夠看到頂面的立方體，標記爲4；

第3層，有2個能夠看到頂面的立方體，分別標記爲3；

第2層，也是2個能夠看到頂面的立方體，分別標記爲2；

第1層，沒有任何能夠看到頂面的立方體，所以代表第一層沒有新的列，無需標記任何數字。（這一步，孩子容易出錯，一定是看到頂面，而不是看到側面。）

最終的結果，就是所有列個數的相加，也就是標記的數字相加：4+3+3+2+2=14（個）。

這個方法，也是最快速的方法。

方法二：按層計算

這個方法，稍微複雜一些，但是可以檢驗自己做得對不對，也有部分孩子會覺得第一種方法不太好理解，那麼也可以試試第二種方法。

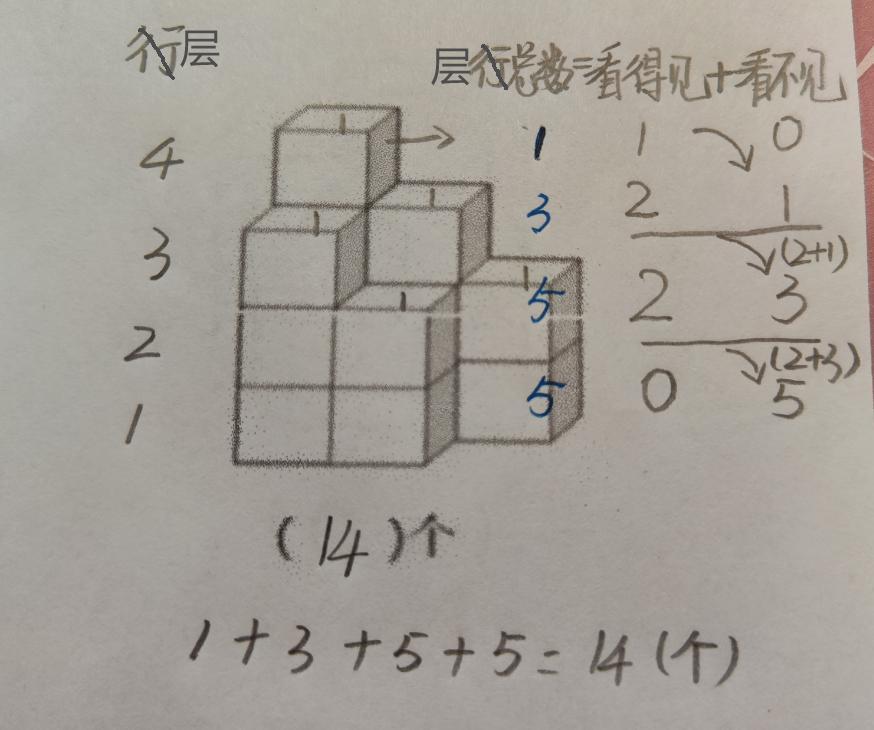
同樣，從下往上標記層數，我們從最頂上一層開始計算。

這個方法有一個簡單的計算公式，那就是：每層總數+看得見+看不見。

看得見的，就是這一層能夠看得到頂面的立方體，看不見的其實就是上一層的立方體，因爲被上一層的擋住了，所以看不見。兩者相加，便是一層的總數。

第4層：一共有1個看得見的立方體，標記1，計數1；

第3層：一共有2個看得見的立方體，再加上看不見的立方體個數，是第4層的立方體數量，爲1，所以第3層一共有2+1=3（個）。

第2層：一共有2個看得見的立方體，再加上第3層有3個立方體，是第2層看不到的，第2層就一共有2+3=5（個）。

第1層：沒有能夠看得到頂面的立方體，所以這一層的立方體總數，便是被第2層遮擋的5個立方體。

最終，一共有1+3+5+5=14（個）。

驗證結果：從結果看無論是從層還是從列來計數，都是14個立方體，這個答案正確！

話題討論：這類題目，你還有更好的解法嗎？

（後附練習，有需要的家長可自取）