量子計算機爲什麼能加速計算?
我們可能頻頻在科技新聞中聽到“量子”“量子計算機”這樣的名詞,也有一個模糊的感覺,那就是“量子計算機”比普通的計算機更快,但快在哪兒,爲什麼快,就說不出個所以然了,而今天咱們就來系統地講講量子計算機爲何“快”。
量子計算機的核心優勢在於其利用了量子疊加性和量子糾纏性。爲了理解其對計算的加速,首先需要了解量子物理的基礎特性——疊加態、坍縮和量子糾纏。
疊加態與坍縮
在經典物理中,系統的狀態(例如位置、速度)在任意時刻都是確定的;而在量子力學中,粒子的情況則不同。一個粒子的某一物理量(如位置、動量、自旋、能級等)在未被測量之前,並不處在某一個具體的值,而是一個同時包含所有可能的結果的疊加態。只有在測量時,這個疊加態纔會按照某種概率瞬間變成某個固定的值。
舉一個簡單的例子:設想有兩個小盒子,粒子只能出現在其中一個盒子裏。按照經典的直覺,它要麼在左邊的盒子裏,要麼在右邊的盒子裏,永遠不會同時在兩個地方。但在量子實驗中發現,在沒有測量之前,粒子並不是已經待在左邊或者右邊,而是處在一種同時“包含左和右可能性”的狀態。
只有當我們真正去測量時,粒子纔會呈現爲在其中一個盒子裏。這個過程叫做坍縮。坍縮時,每一個可能的狀態都會對應一個概率(概率需滿足所有可能性的總和爲 100 %,具體的概率分佈是疊加態的性質之一)。例如,一個粒子可能處在如下的疊加態:
· 出現在左邊的概率爲 70%
· 出現在右邊的概率爲 30%
這聽起來似乎難以置信,但疊加態的存在早已通過實驗得到驗證,一個經典的例子就是電子的雙縫干涉實驗,感興趣的讀者可以進一步查閱相關實驗。
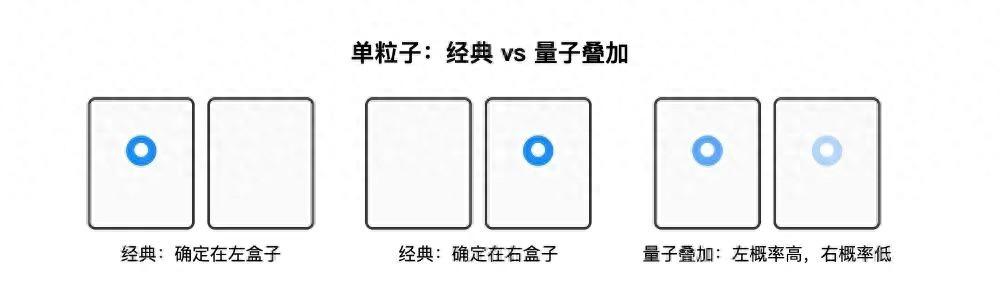
圖1經典物理狀態與量子疊加態的對比,量子疊加態的顏色代表其在測量時出現的概率。
基於這一原理,量子計算機從物理系統中選擇兩個可以明確區分的結果來作爲信息的基本單位。例如,可以規定“粒子在左盒子裏”爲 0,“粒子在右盒子裏”爲 1。這樣,一個量子比特在未被測量時,並不是單純的 0 或 1,而是同時包含兩種可能性。當測量發生時,它纔會確定爲其中之一。這意味着,量子比特能夠在未測量時以疊加的形式同時攜帶 0 和 1 的信息,這是它區別於經典比特的根本特徵。
量子糾纏
在理解了單個物理量可以同時處於多種可能性的疊加之後,我們就可以進一步討論量子糾纏。量子糾纏是一種超越經典直覺的量子關聯現象。當兩個或多個粒子的某些屬性(例如它們所在的位置)發生糾纏時,這些屬性不再是彼此獨立的,而是形成一個不可分割的整體。
舉個例子:設想有兩隻相同的小盒子,一個在左邊,一個在右邊。我們現在放入兩個粒子,分別編號爲 1 號和 2 號。按照經典的直覺,可能的情況有四種,每種都有一定的發生概率:
· 兩個粒子都在左邊(記作 “LL”);
· 兩個都在右邊(“RR”);
· 1 號在左、2 號在右(“LR”);
· 1 號在右、2 號在左(“RL”)。
經典物理會認爲,粒子一定處於其中一種確定的組合,只是我們暫時不知道是哪一種。
但在量子物理中,如果兩個粒子的位置發生了“兩個粒子所在的盒子必須不同”的糾纏,那麼情況就完全不同。在測量之前,它們並不是已經固定在某一種組合,而是處在一種整體性的疊加狀態。在這種狀態下,只允許兩種可能性同時存在:
· 1 號在左、2 號在右(“LR”);
· 1 號在右、2 號在左(“RL”)。
當我們真正去測量時,系統會瞬間“坍縮”爲其中之一:要麼是“LR”,要麼是“RL”。每一種情況都有一個對應的概率(概率不必相等,概率分佈是糾纏態的固有性質之一)。與此同時,“LL”與“RR”的結果概率爲零。可以看出,糾纏後的量子態其實是一個更爲全局的疊加態。量子糾纏也是通過物理實驗得到驗證的,感興趣的讀者可以進一步查閱相關資料(關鍵詞:EPR 佯謬,貝爾不等式)。
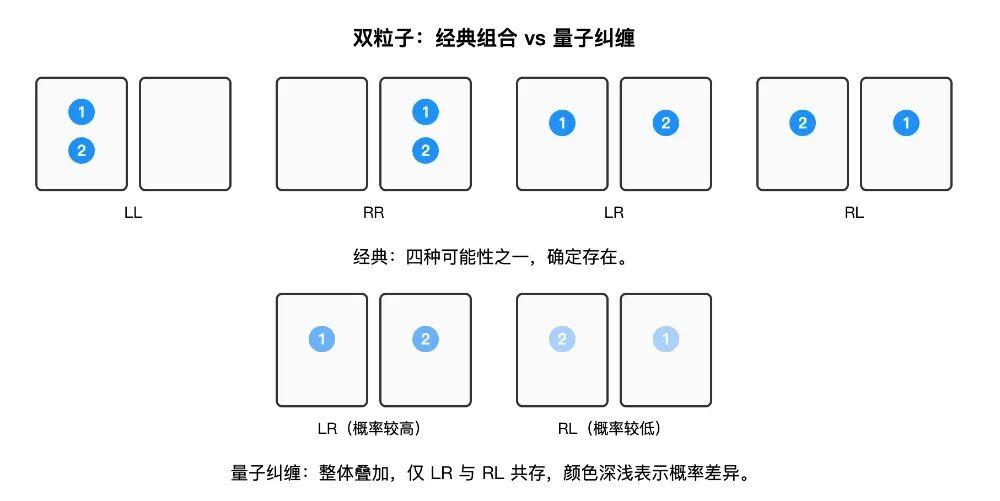
圖2經典粒子組合與粒子糾纏之間的對比
將這一原理應用到量子比特上(比如我們認爲 L 爲 0,R 爲 1),我們就可以製備出一種“兩個比特的取值必須不同”的糾纏狀態。在這種狀態下,兩個比特在測量之前,並不是確定地處在“01”或者“10”,而是這兩種可能性的疊加。等到測量發生時,系統會瞬間坍縮爲某一個確定的結果:要麼得到“01”,要麼得到“10”。與此同時,“00”與“11”這兩種組合完全不會出現,它們的概率爲零。
利用疊加性和糾纏性加速計算
疊加性賦予量子比特在未測量時同時處於多種狀態的能力,糾纏性使得量子比特之間能夠形成非經典的強關聯,這種關聯在許多量子算法和量子誤差校正中是不可或缺的核心資源。
在這裏,我們給出一個直觀的例子來幫助理解。假設我們有一個由 n 個量子比特組成的系統,用它來表示一個輸入變量 x。由於疊加原理,x 的狀態可以同時覆蓋從 0 到 2^n-1 的所有可能取值,而不僅僅是某一個具體數。當我們將這樣的量子態輸入到函數 f(x) 中時,輸出也會成爲所有可能輸入對應結果的疊加態。
如果我們想尋找滿足f(x)=c 的 x 的值,就可以通過精心設計的量子算法(涉及對量子糾纏和量子干涉等機制的利用),增強正確結果對應的概率振幅,同時削弱錯誤結果的概率振幅。這樣,在最終測量時,就能夠以更高概率得到正確答案。需要強調的是,這種“放大正確解概率”的過程,正是量子算法的核心思想之一。
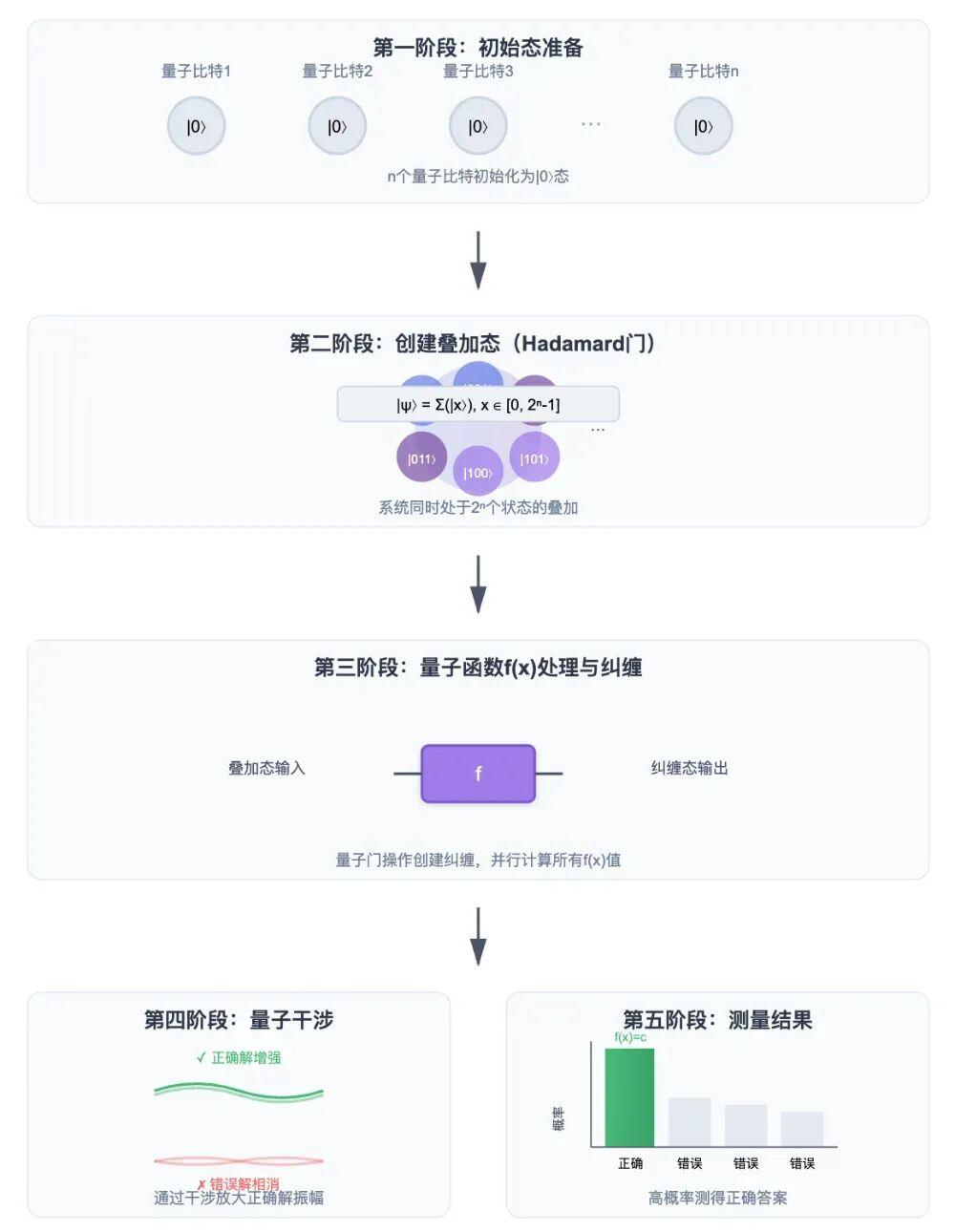
圖3量子計算的核心思想,通過疊加實現並行計算,通過糾纏和干涉放大正確解的概率
注:在提到量子干涉時,我們實際上默認了量子態可以用波的形式來表示。爲了照顧不熟悉數學或物理的讀者,我沒有展開說明這一點。

圖4干涉是波的疊加效應。當兩個正弦波的波峯重合時,會產生相長干涉,疊加後的振幅增大;反之,則會發生相消干涉,振幅減小。我們所熟悉的降噪耳機就是利用相消干涉來抵消噪音,量子計算也可以通過相長干涉放大正確答案的概率振幅,通過相消干涉縮小錯誤答案的振幅。
當然,現實中的量子算法遠比這個直觀描述複雜得多,這裏我們僅作簡化說明,暫不涉及具體算法細節。
量子計算對不同問題的加速效果
量子計算機所帶來的加速的主要來源是:
· 疊加態,即 n 個量子比特可以同時表示 2ⁿ 個狀態。
· 糾纏,通過量子比特間的強關聯,使不同狀態間發生干涉,從而有效提取有用信息、放大正確答案。
需要注意的是,量子計算機並不是像經典的計算機那樣直接並行處理所有可能性並輸出全部結果,而是依賴於量子干涉和算法設計,用於放大正確答案的概率,這使得量子計算機能夠實現對複雜問題的高效求解。
而量子計算機在加速在不同類型的問題上體現得不同,在合適量子算法的情況下:
· 有結構的問題(如質因數分解):量子算法可以利用其結構(如週期結構),通過某種算法(如量子傅里葉變換)快速提取答案,從而實現 指數級加速。
· 無結構的問題(如尋找滿足 f(x)=c 的 x):由於沒有規律可利用,只能依靠連續 √N 次干涉放大正確答案的概率幅,因此計算次數只能從經典的 N 次降到 √N 次,對應 平方根級加速。
好了,以上就是量子計算機的基本原理了,簡單來說,量子比特能同時承載多種可能,再通過算法篩選出最優解。這樣的特性,讓量子計算機在特定複雜問題(如質因數分解或大規模搜索)上的運算速度遠超傳統計算機。但量子計算的也並非萬能,理解這些基礎原理,能幫我們更清醒地看待這項技術的潛力與侷限。
策劃製作
本文爲科普中國·創作培育計劃扶持作品
出品丨中國科協科普部
監製丨中國科學技術出版社有限公司、北京中科星河文化傳媒有限公司
作者丨李冠成 騰訊玄武實驗室
審覈丨欒春陽 中國移動通信研究院未來研究院 研究員
策劃丨張林林
責編丨丁崝
審校丨徐來 張林林