量子力學和宏觀世界的次元壁,再次被這三位諾獎得主打破了
點擊圖片進入歷年諾貝爾獎解讀合集
作者 | 施鬱(復旦大學物理學系)
剛剛,2025年諾貝爾物理學獎頒佈,約翰·克拉克(John Clarke)、米歇爾·德沃雷(Michel H. Devoret)和約翰·馬丁尼斯(John M. Martinis)獲獎,表彰他們發現了電路中的宏觀量子力學隧穿和能量量子化現象。
人們常常調侃,“遇事不決,量子力學”。量子力學自上世紀初誕生以來,完美地解釋了微觀世界的無數現象,但在我們肉眼可見的宏觀世界中,純粹的量子現象卻極爲罕見。
而正是依靠本年度諾獎得主的卓越貢獻,人類首次在由數十億電子組成的宏觀電子電路中,捕捉到了量子力學中最奇特、最迷人的現象之一——量子隧穿效應。
什麼是量子隧穿?爲什麼電子會像幽靈一樣“穿牆而過”?三位諾獎得主又是如何通過深刻的理論思考和精巧的實驗設計,成功將原本只屬於微觀粒子的量子行爲,帶入了人類的電路?
本文將帶您回顧這一重要科學發現的歷史背景與發展歷程,從中領略三位諾獎得主的劃時代貢獻。
超導和超流
超導和超流經常被稱作“宏觀量子現象”。但是通常情況下,它們只是微觀量子行爲的宏觀表現,並不是宏觀變量的量子化。

超導懸浮

液氦超流
按照統計性質,量子粒子分爲兩種。一種叫做玻色子,可以處於相同狀態。另一種叫做費米子,任何兩個費米子都不能處於相同狀態。在量子力學中,同種粒子,比如兩個電子或者兩個光子,是絕對完全一樣的,叫做全同粒子。由2個質子和1箇中子組成的原子核叫做氦3原子核,它與2個電子組成電中性的氦3原子,是費米子。由2個質子和2箇中子組成的原子核叫做氦4原子核,它與2個電子組成電中性的氦4原子,是玻色子。
因此在系統總能量最低時,簡單來說(忽略相互作用),大量的全同玻色子都處在相同的最低能量狀態,叫做玻色-愛因斯坦凝聚。超流就是玻色-愛因斯坦凝聚的後果。最常見的超流是氦4超流。
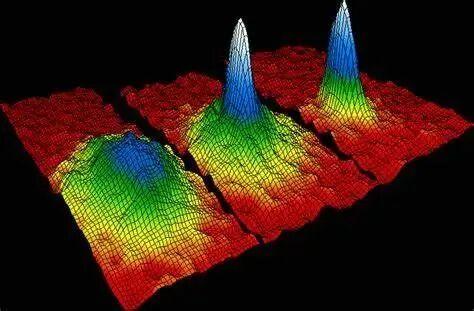
玻色-愛因斯坦凝聚
而費米子可以由某種機制導致兩兩配對,形成“庫珀對”,近似於玻色子。庫珀對的近似玻色-愛因斯坦凝聚也導致超流。最常見的費米子超流是固體中的電子超流,一般稱作超導電性(因爲電子帶電),簡稱超導。也存在電中性的費米子超流,如氦3的超流。
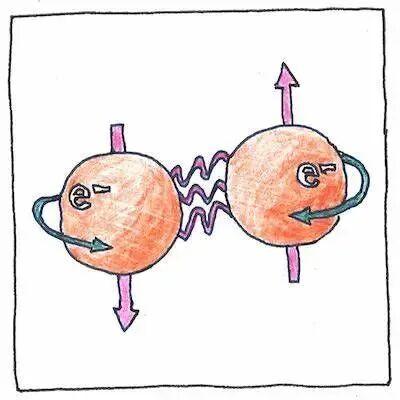
庫珀對卡通示意圖
基於庫珀對凝聚的超導理論於1956年由巴丁(John Bardeen),庫珀(Leon Cooper)和施裏弗(John Robert Schrieffer)提出,庫珀對的總自旋(內稟角動量)爲0。而氦3超流的庫珀對總自旋爲1。對氦3超流的理論做出貢獻的萊格特(Anthony J. Leggett)因此獲得2003年諾貝爾物理學獎。安德森(Philip Anderson)等人對此也有重要貢獻。
玻色-愛因斯坦凝聚、超流或者超導都可以由一個序參量描寫,有時被稱爲宏觀波函數,它是一個複數函數。粒子之間作用力比較弱時,可以用平均場理論來描述,假設所有全同粒子的波函數一樣,它們相乘在一起,就構成系統的整體波函數。每個全同粒子的單體波函數就是序參量(通常再乘以粒子數的平方根)。對於相互作用較強的情況,序參量是規範對稱自發破缺所導致的場算符的期望值,或者是單玻色子或者雙費米子約化密度矩陣的最大本徵值的本徵函數(這個說法對應於Penrose-Onsager和楊振寧的非對角長程序)。
不管理論上以何種方式得到,這個序參量(或稱宏觀波函數)的一個重要特徵是相位。相位隨着位置的變化驅動了超流。約瑟夫森效應體現了這個相位的物理真實性。對於由絕緣體薄層隔開的兩個超導體,兩個超導體的宏觀波函數的相位差直接導致穿過絕緣體的超導電流,電流強度正比於相位差的正弦函數,這就是約瑟夫森效應。它是劍橋大學研究生約瑟夫森(Brian Josephson)在學習Philip Anderson的超導課程時,用多體微觀理論得到的結論。宏觀波函數的相位差是一個宏觀變量,但是由於粒子數漲落很大,相位成爲一個經典變量。
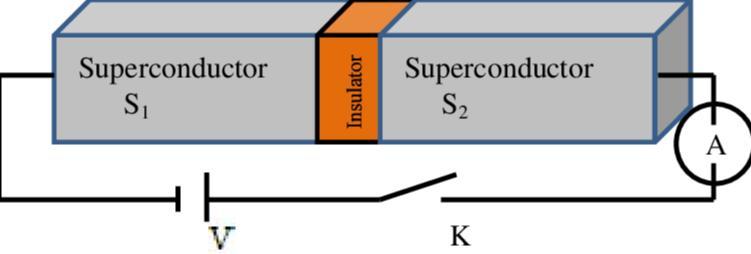
約瑟夫森結
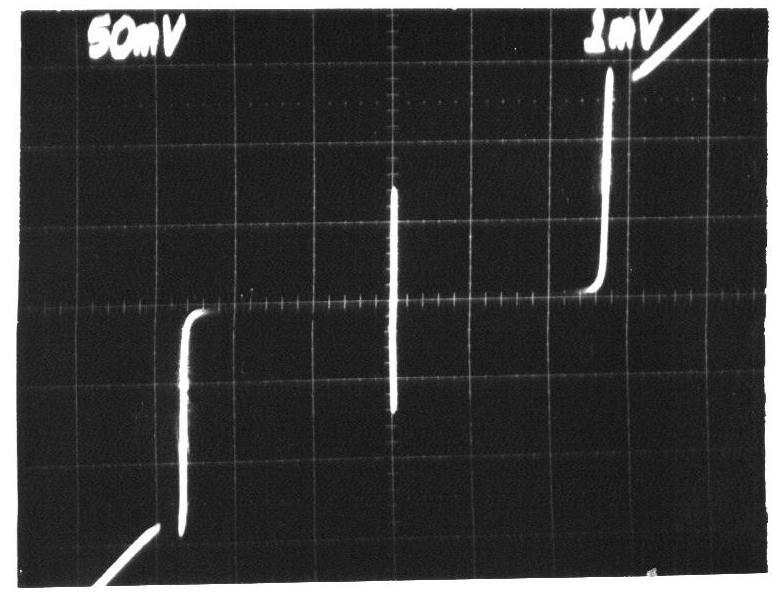
約瑟夫森結的 I-V 曲線
粒子數與相位是量子共軛算符
對於小約瑟夫森結,相位也有漲落,粒子數與相位都成爲量子力學算符,而且它們具有共軛關係,類似位置和動量之間的關係,也就是互不對易(改變作用順序,結果不同)。這也使得它們之間也服從海森堡的不確定關係。
1980年,Leggett指出[1],通常所謂的“宏觀量子系統”,即超導和超流,以及磁通量子化和約瑟夫森效應這些後果,並沒有表明量子力學原理適用於宏觀系統,因爲其中並沒有宏觀上的不同狀態之間的量子疊加(如假想的薛定諤貓),但是由於在超導或超流狀態下,耗散低,超導器件特別是SQUID(超導量子干涉儀,即具有兩個約瑟夫森結的超導環),通過特別的設計,適合於尋找不同宏觀狀態之間的量子疊加或量子隧穿。這引領了幾十年約瑟夫森結的量子效應的研究,包括超導量子比特的興起。

作者與Leggett教授(攝於2003年10月諾貝爾獎宣佈後伊利諾伊大學立即爲Leggett舉行的慶祝會)
約瑟夫森結量子行爲的首次實驗觀察
1985年,加州大學伯克利分校John Clark教授帶領兩位學生John Martinis和Michel Devoret,首先觀察到偏電流約瑟夫森結的量子行爲[2]。偏電流是指外電流。具體來說,他們觀察到量子化的能級,表明了約瑟夫森結的相位差確實是一個量子力學算符,實驗結果與理論一致。
描述這個系統的方程類似於一個質點的一維運動,約瑟夫森結相位差對應於質點位置。對應後,質點所受的勢能作爲位置的函數,是傾斜的餘弦函數。在約瑟夫森結中,這個傾斜由偏電流引起。約瑟夫森結的零電壓態對應於質點的勢能低點(叫做勢阱)。量子力學預言,在勢阱中,質點處於所謂束縛態(指束縛在勢阱中),而且所能具有的能量是分立的,叫做能級——也就是說,只有某些特定的數值才被允許,這叫能量量子化。原子中的電子就具有這個性質。具有如此能級結構的人工器件有時被稱作人造原子,可以用約瑟夫森結實現,也可以用半導體量子點實現。
Clarke和兩位學生將約瑟夫森結用微波輻照,發現當微波頻率(乘以普朗克常數)等於分立能級之差時(幾個GHz),“質點”逃逸率(逃逸出勢阱的概率)大大增加,也就是說,約瑟夫森結兩端的電壓以及導致的電流大大增強。這是一種共振,類似於,如果電磁波的頻率(乘以普朗克常數)與原子中的電子能級差相等,低能級的電子就會吸收光子,躍遷到高能級。他們觀測到,隨着溫度升高,逃逸率從量子共振激發過渡到經典熱激發。
就這樣,約瑟夫森結的量子行爲首次得到證明,而且表明可以通過電路對它進行控制,並能將多個約瑟夫森結連結起來。短短兩年後,Clark因此獲得了低溫物理的菲列茲·倫敦獎(Fritz London Memorial Prize)。
他們的約瑟夫森結材料是Nb-NbOx-PbIn,中間的氧化鈮是絕緣體,兩邊的鈮和鉛銦合金是超導體。後來人們改用Al-Al2O3-Al, 即鋁-氧化鋁-鋁,它的耗散更低[3]。
小約瑟夫森結
約瑟夫森結的能量來自兩個互相競爭的部分。一是庫珀對帶來的充電能,等於充電能常數(一對庫珀對的充電能)乘以庫珀對數目(減去一個所謂的門電荷數)的平方。另一個是約瑟夫森隧道耦合能,是庫珀對隧穿導致的負能量(當庫珀對波函數是隧道兩邊的疊加態時,能量降低),等於負的約瑟夫森能量常數(臨界電流乘以磁通量子,除以2π)乘以相位差的餘弦。
1990年代,很多研究組研究小約瑟夫森結[4]。代爾夫特工業大學的J. E. Mooij組研究了約瑟夫森結陣列[5],哈佛大學的Tinkham組觀察到超導單電子晶體管的電流-電壓關係中的2e週期性[6],當時在法國Saclay原子能委員會的Devoret組也證實了這個結果[7],J. E. Mooij組證明了相位與電荷(庫珀對數目乘以電子電荷)之間的海森堡關係[8]。
量子計算的興起
1980年代,量子計算的研究開始出現。1990年代早期,Peter Shor提出可以有效解決因子化問題的量子算法,使得量子計算得到更廣泛的關注。當時,量子計算的物理實現主要在光子、離子、原子這些系統中研究,而固體物理系統被認爲太複雜,自由度太多。1990年代後期,研究超導約瑟夫森結和半導體量子點的科學家開始對量子計算感興趣,試圖實現量子比特。當時仍然有很多科學家不知道這個領域。記得世紀之交時,筆者向一位知名凝聚態理論學者說起對凝聚態系統中的量子糾纏與量子計算實現有點興趣,對方不知道什麼意思。
固態“人造原子”有其優點,它可以藉由電路實現仔細的調控,因爲相對於真正的原子,更容易調控各種參數,而且也容易和傳統的技術整合,便於擴展到很多量子比特。
任何用來實現量子計算的物理系統,首先要解決的問題是量子比特的物理實現,包括單個量子比特以及不同量子比特的耦合。下文主要回顧單個超導量子比特的實現。
超導量子比特
超導量子比特有很多種。當充電能比約瑟夫森能大很多時,相位漲落大,庫珀對數目接近明確,所實現的量子比特叫做電荷量子比特,又叫庫珀對盒子。當約瑟夫森能比充電能大很多時,粒子數漲落大,相位明確,所實現的量子比特叫做相位量子比特,也可實現磁通量子比特。另外還有quantronium, transmon, flxonium,等等。
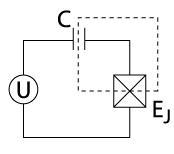
電荷量子比特
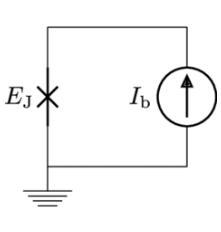
相位量子比特
1998年,Devoret組證明了電荷量子比特疊加態的存在性[9]。
1999年,當時在日本NEC實驗室的中村泰信及其合作者Pashkin和Tsai實現了電荷量子比特的疊加態[10]。他們用電壓脈衝,實現了相差一對庫珀對的兩個粒子數本徵態的量子疊加。雖然相干時間(維持疊加態的時間)只有2納秒,但是脈衝時間只有100皮秒。後來,他們又實現了在微波作用下,這兩個電荷本徵態之間的拉比振盪[11]。
2000年,紐約州立大學石溪分校的Lukens組[12]和代爾夫特的Mooij組[13]分別在特別設計的、包含3個約瑟夫森結的超導環中,實現了不同電流方向(順時針和逆時針)的量子疊加態。這也叫磁通量子比特,因爲兩個方向的電流對應不同的、穿過環路的磁通量。但是量子疊加的證據是間接的,來自光譜[14]。
2002年,在Saclay和耶魯大學的Devoret組用圍繞一個庫珀對盒子巧妙設計的超導電路,以哈密頓量的兩個本徵態作爲量子比特,實現了任意幺正演化(包括拉比振盪)以及投影測量[15]。他們自己稱這個量子比特爲quantronium。這是電荷-磁通混合量子比特[14],自由演化時,對電荷和磁通噪聲都不敏感,等效於電荷量子比特,而讀出時又改變控制參數,對磁通敏感,等效於磁通量子比特。
與之同時,堪薩斯大學的韓思遠組發表了偏電流約瑟夫森結的兩個本徵態之間的拉比振盪[16]。當時在科羅拉多的NIST的Martinis組也觀察到同樣的現象。偏電流約瑟夫森結也就是1985年Clarke、Martinis和Devoret最初研究的系統,它的兩個本徵態對磁通噪聲敏感度低於磁通量子比特[14]。它們被稱爲相位量子比特[18,19],因爲約瑟夫森能比充電能大很多。
2003年,Mooij組實現了磁通量子比特的拉比振盪和讀出[20]。當時中村泰信在該組訪問,是該工作的合作者。
後來這個領域又取得了長足的進展,包括雙量子比特和多量子比特的耦合,直到最近用幾十個量子比特實現量子優越性[21,22]。這裏不再贅述。
置於微波腔中的超導量子電路還導致所謂電路量子電動力學,電磁波顯示出量子行爲。比起基於腔量子電動力學(原子與光子耦合)的量子門和讀出,基於電路量子電動力學的量子門和讀出快1000倍,但是退相干也快1000倍,不過電路量子電動力學能獲得大量數據[3]。
Leggett一直在推動用SQUID檢驗是否存在宏觀不同的狀態的量子疊加[23]。最近的一個磁通量子比特實驗說明,至少對於10納秒、170納安培的電流,存在兩個方向電流狀態的量子疊加[24]。
小結
通過我們的回顧綜述,可以看到,J. Clarke和他的學生J.M.Martinis和M.H. Devoret最早通過偏電流約瑟夫森結,首次觀察到約瑟夫森結的量子行爲。後來Devoret又做了一系列工作,包括1998年證明了電荷量子比特疊加態的存在性, 2002年實現電荷-磁通混合量子比特的拉比共振和其他演化及投影測量。中村泰信1999年和2001年分別首先實現超導量子比特的量子疊加和拉比振盪,是在電荷量子比特中。他2003年還參與Mooij組實現了磁通量子比特的拉比振盪和讀出。
參考文獻
[1] A.J. Leggett, Macroscopic quantum systems and the quantum theory of measurement, Progr. Theor. Phys. (Suppl.) 69 (1980), 80
[2] J.M.Martinis, M.H. Devoret and J. Clarke, Energy level quantization in the zero-voltage state of a current-biased Josephson junction, Phys. Rev. Lett. 55 (1985), 1543
[3] J.M.Martinis, M.H. Devoret and J. Clarke, Quantum Josephson junction circuits and the dawn of artificial atoms, Nature Physics volume 16, pages234–237 (2020)
[4] J. E. Mooij, The first Delft qubit, QuTech Blog.
[5] L.J. Geerligs, M. Peters, L.E.M. de Groot, A. Vebruggen and J.E. Mooij, Charging effects and quantum coherence in regular Josephson junction arrays, Phys. Rev. Lett. 63 (1989), 326
[6] M.T. Tuominen, J.M. Hergenrother, T.S. Tighe and M. Tinkham, Experimental evidence for parity-based 2e periodicity in a superconducting single-electron tunneling transistor, Phys. Rev. Lett. 69 (1992), 1997
[7] P. Lafarge, P. Joyez, D. Esteve, C. Urbina and M.H. Devoret, Two-electron quantization of the charge on a superconductor, Nature 422 (1993), 422
[8] W.J. Elion, M. Matters, U. Geigenmüller and J.E. Mooij, Direct demonstration of Heisenberg’s uncertainty principle in a superconductor, Nature 371 (1994) 594
[9] Quantum coherence with a single Cooper pair, V. Bouchiat, D. Vion, P. Joyez, D. Esteve and M.H. Devoret, Physica Scripta T76 (1998), 165
[10] Y. Nakamura, Yu.A. Pashkin and J.S. Tsai, Coherent control of macroscopic quantum states in a single-Cooper-pair box, Nature 398 (1999), 786
[11] Y. Nakamura, Yu.A. Pashkin and J.S. Tsai, Rabi oscillations in a Josephson-junction charge two-level system, Phys. Rev. Lett. 87 (2001), 246601
[12] J.R. Friedman, V. Patel, W. Chen, S.K. Tolpygo and J.E. Lukens, Quantum superposition of distinct macroscopic states, Nature 406 (2000), 43
[13] C.H. van der Wal, A.C.J. ter Haar, F.K. Wilhelm, R.N. Schouten, C.J.P.M. Harmans and J.E. Mooij, Quantum superposition of macroscopic persistent-current states, Science 290 (2000), 773
[14] A. J. Leggett, Superconducting Qubits--a Major Roadblock Dissolved? Science 296 (2002), 861-862
[15] D. Vion, A. Assime, A. Collet, P. Joyez, H. Pothier, C. Urbina, D. Esteve and M.H. Devoret,Manipulating the quantum state of an electrical circuit, Science 296 (2002), 887
[16] Y. Yu, S. Han, X. Chu, S.-I Chu, Z. Wang, Coherent Temporal Oscillations of Macroscopic Quantum States in a Josephson Junction, Science 296 (2002), 889-892
[17] J.M. Martinis, S. Nam and J. Aumentado, Rabi oscillations in a large Josephson-junction qubit, Phys. Rev. Lett. 89 (2002), 117901
[18] J. Clarke, Flux qubit completes the hat trick, Science 299 (2002), 1850
[19] J. Q. You and Franco Nori, Superconducting Circuits and Quantum Information, Physics Today, November 2005, 42-47
[20] I. Chiorescu, Y. Nakamura, C.J.P.M. Harmans and J.E. Mooij, Coherent quantum dynamics of a superconducting flux qubit, Science 299 (2003), 1865.
[21] F. Arute, et al., Quantum supremacy using a programmable superconducting processor, Nature, 574, 505 (2019).
[22] Y. Wu et al., Strong quantum computational advantage using a superconducting quantum processor, Phys. Rev. Lett. 127, 180501 (2021).
[23] A. J. Leggett,公衆演講:“日常世界真的服從量子力學嗎?”,主持並翻譯:施鬱,對話嘉賓:潘建偉、陳宇翱,2020年12月27日,
https://www.cdstm.cn/subjects/kjgldkxk/kxkzb/kxlx/202012/t20201221_1039348.html
[24] George C. Knee, Kosuke Kakuyanagi, Mao-Chuang Yeh, Yuichiro Matsuzaki, Hiraku Toida, Hiroshi Yamaguchi, Shiro Saito, Anthony J. Leggett & William J. Munro, A strict experimental test of macroscopic realism in a superconducting flux qubit, Nature Communications volume 7, Article number: 13253 (2016).
快來關注,不要錯過!

點擊圖片進入歷年諾貝爾獎解讀合集
本文經授權轉載自墨子沙龍(ID:MiciusSalon