小學新教材引發熱議，3×8不等於8×3了？幸好畢業早啊！

最近一則小學數學教學引發熱議，其中新教材下3×8≠8×3的情況違反我們的直覺。

這樣的現象出現其實源於對乘數和被乘數的定義，在小學數學的語境中，3×8其實對應着“一個人有3個蘋果，現在一共有8個人”，而8×3則對應“一個人有8個蘋果，現在一共有3個人”。

圖文無關......

在數學的廣闊天地中，運算的順序有時無關緊要，有時卻決定一切。我們從小就熟知 3 + 5 等於 5 + 3，這種運算順序的可交換性看似理所當然，但它實際上是通往兩類深刻數學結構——阿貝爾羣與非阿貝爾羣——的分水嶺。

用更數學的角度來考慮，其實乘法交換律是否成立更根本的本質，是該運算下羣是否構成的阿貝爾羣。而其實很多的數學理論中的乘法運算是不滿足交換律的，接下來就跟着小編一起去看看走近非阿貝爾羣的世界！

從小學乘法開始

小學學到的乘法交換律是定義在自然數的數域內。對於自然數，我們要想嚴格得乘法交換律的證明是，我們要從皮亞諾公理開始。

皮亞諾公理給出了自然數形式化的定義。如果感興趣的朋友不難發現，皮亞諾公理的定義有着歸納遞推的思想，沿着這個思想可以得到加法和乘法的定義：

1. 對於任何正整數a，定義a×1 =a。

2. 對於任何正整數a和b，定義a×（b+1）= a×b+a。

在此定義下我們分別可以推導得到乘法分配律和乘法交換律，感興趣的同學可以看看下圖給出的推導思路。

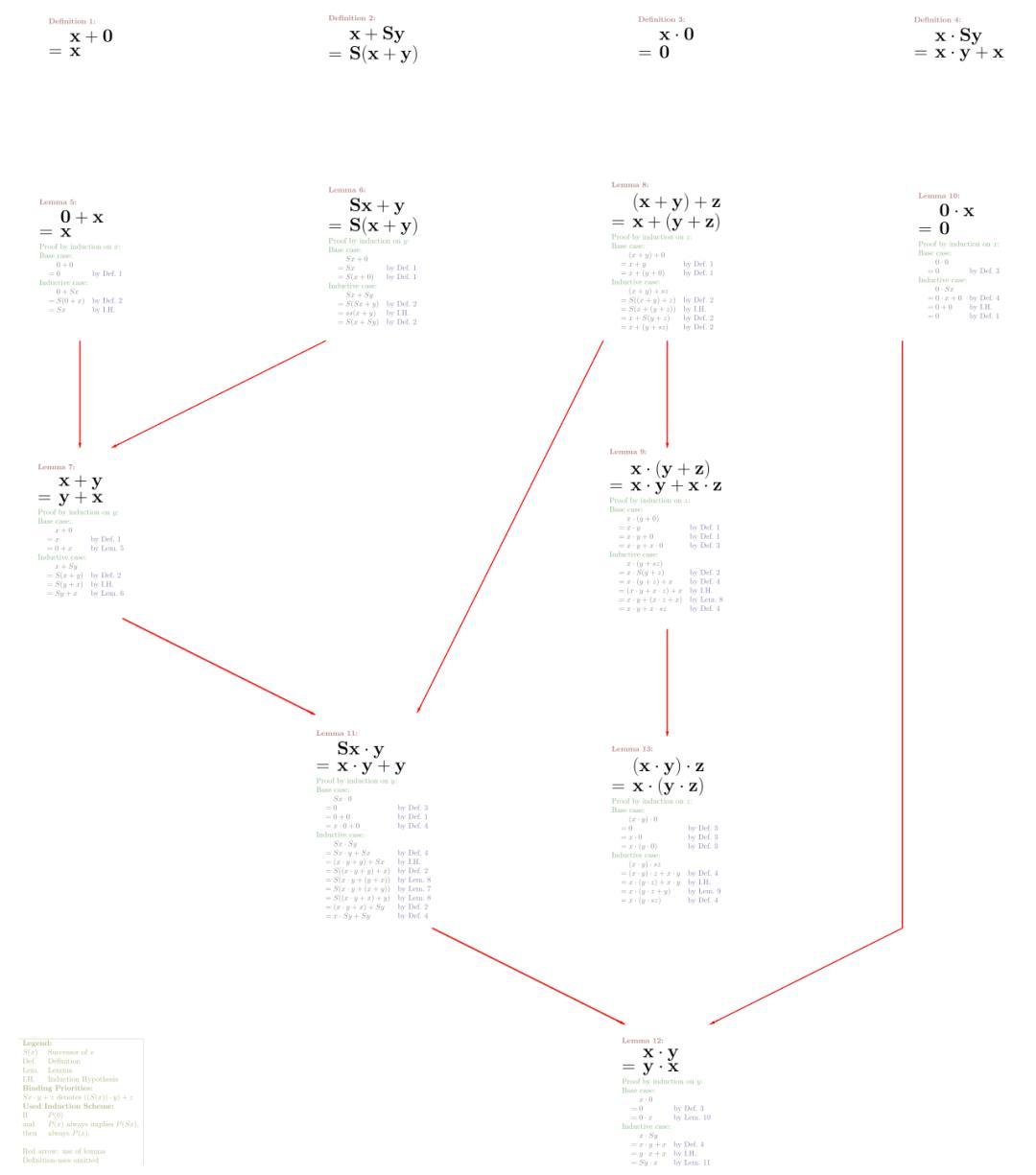
原圖：
https://upload.wikimedia.org/wikipedia/commons/3/34/Inductive_proofs_of_properties_of_add%2C_mult_from_recursive_definitions_svg.svg

從小學到高中我們都沿着乘法交換律的路學習着數學知識，教科書上的數學內容也都是在交換律成立的範圍內，直到遇到了高中物理所學到的帶電粒子在磁場中的受力公式：

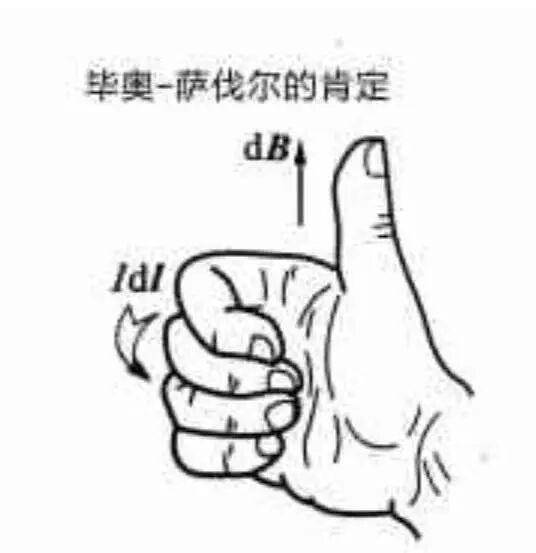
這裏用到的就是向量運算中的叉乘，這類運算是不符合乘法交換律的。

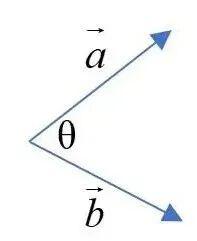
而向量的叉乘運算爲， ,向量大小滿足： ，向量叉乘的積仍爲向量，其方向根據右手螺旋定則確定。

雖然在教科書中沒有詳細敘述叉乘，但是依然讓當年的小編萌生不少疑問。

而進一步大學教授的矩陣運算更是違犯交換律最好的例子，這也揭開了非阿貝爾羣的面紗。

進入羣的世界

在深入探討差異之前，我們首先需要理解它們共同的身份：羣。在抽象代數中，一個羣是一個集合及其上定義的一種運算的組合，這個組合必須滿足四個基本規則，以確保其結構是穩定和自洽的：

封閉性：集合中任意兩個元素通過該運算得到的結果，仍然是這個集合的成員。

結合律：(a × b) × c 的結果與 a × (b × c) 相同，運算的組合順序不影響最終結果。

單位元：集合中存在一個單位元，任何元素與它運算都保持不變（例如，加法中的 0 或乘法中的 1）。

逆元：對於集合中的每一個元素，都存在一個與之對應的“抵消”元素，兩者運算後會得到單位元（例如，a 的逆元是 -a，因爲 a + (-a) = 0）。

同時滿足這四條公理的系統，就是一個“羣”。它爲數學家提供了一個研究對稱性和變換的強大框架。

當一個羣的運算不僅滿足以上四條規則，還滿足交換律(a * b = b * a) 時，它就被稱爲阿貝爾羣（或交換羣），以紀念挪威數學家尼爾斯·阿貝爾。

阿貝爾和橢圓函數理論

阿貝爾羣在數學中無處不在，例如：

整數加法羣 (ℤ, +)：所有整數在加法下構成一個完美的阿貝爾羣。

非零實數乘法羣(ℝ*, *)：所有非零的實數在乘法下同樣構成阿貝爾羣。

當交換律被打破，即羣中至少存在一對元素使得 a * b ≠ b * a，我們就進入了非阿貝爾羣的領域。這些羣描述了更加複雜、順序至關重要的現象。

最直觀的例子來自於矩陣和幾何變換：

• 一般線性羣 GL(n, ℝ)：所有 n×n 可逆實數矩陣在矩陣乘法下構成的羣。當 n≥2 時，這是一個經典的非阿貝爾羣，因爲矩陣乘法通常不滿足交換律。

• 三維旋轉羣 SO(3)：我們生活的三維空間中，所有繞原點的旋轉操作構成一個非阿貝爾羣。將一個物體先繞 X 軸旋轉90度再繞 Y 軸旋轉90度，與先繞 Y 軸再繞 X 軸旋轉，物體的最終朝向是截然不同的。

在實際各個領域非阿貝爾羣也有非常重要的作用。

在粒子物理學中，描述基本力的標準模型完全建立在非阿貝爾的規範羣之上。例如，傳遞強相互作用（將夸克綁定在一起）的 SU(3) 羣和傳遞弱相互作用（引起放射性衰變）的 SU(2) 羣都是非阿貝爾的。它們的非交換性直接導致了傳遞力的粒子（如膠子和W/Z玻色子）之間會相互作用，這是構成我們物質世界的關鍵特性。

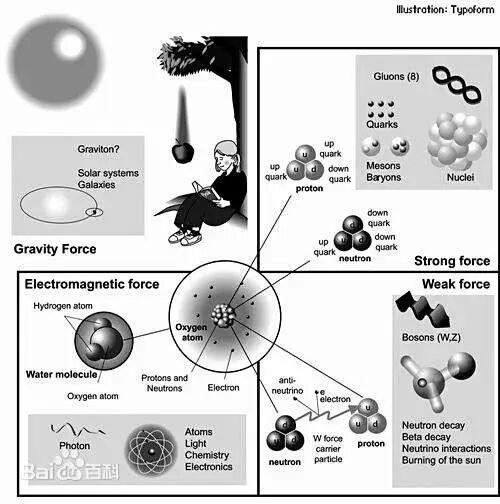
圖源：百度百科

在機器人學和計算機圖形學中，SO(3) 羣被用來精確計算和描述三維空間中物體的姿態和運動軌跡，其非交換性是處理複雜運動規劃和避免“萬向節死鎖”等問題的核心。

再看看生活

其實運算非交換在生活中非常常見。想象一下，你正在執行一個任務清單，上面有兩件事：喫早餐和刷牙。你先喫早餐再刷牙，和你先刷牙再喫早餐，最終的結果顯然是不同的。

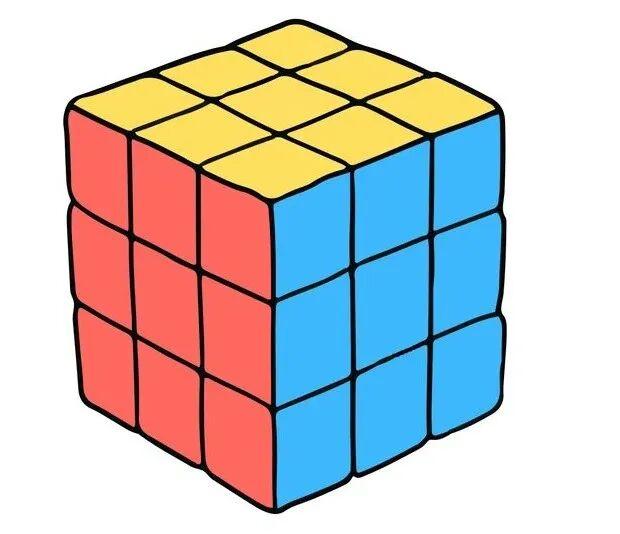
沒有魔方可以對着這個想象......

如果手邊有一個魔方可以嘗試最直觀的非阿貝爾羣變換。分別對魔方進行兩個不同方向的操作A和B，分別執行先A後B和先B後A，你會驚訝地發現，兩種順序執行完，魔方呈現的顏色狀態是完全不同的，魔方的所有可能操作，就構成了一個龐大而複雜的非阿貝爾羣，進而可以想象一下三維空間的旋轉操作也是非阿貝爾的。

所以說下次說到乘法分配律不成立也不要驚訝，先問問運算定義是什麼，再問問乘法作用在什麼樣的數域上。

--End--

參考文獻

[1]Gallian, J. A. (2020). Contemporary Abstract Algebra (10th ed.). Cengage Learning.

[2]李新徵. 羣論及其在凝聚態物理中的應用[M]. 北京大學出版社, 2019.

[3]羣論最大的魅力在於攻克難題的能力，可視化5種最重要的基本羣

[4]https://cameroncounts.wordpress.com/2011/09/21/the-commutative-law/

[5]https://www.zhihu.com/question/285971671

編輯：十一

本文經授權轉載自中科院物理所（ID：cas-iop）