無所不能的奇偶數

想必大家都知道什麼是奇數和偶數，整數中能被2整除的是偶數，反之就是奇數，偶數包括0，2，4，6，……這些雙數，奇數包括1，3，5，7，……這些單數。不過表面上看似平白無奇的奇偶數，其實“暗藏玄機”，在很多意想不到的時候都可以助你一臂之力。

不少人小時候都玩過“一筆畫”遊戲，規則是筆不能離開紙面，起點終點任選，從起點一路畫到終點，每條線都要走過，但又不能重複走第二次，當然每個節點是可以反覆穿過的。對於下面左中右三個圖形，可以試下，是否能夠一筆畫出來？左側和中間的“蝴蝶結”和“橫八字”圖形，應該是“小菜一碟”的任務，參考答案也畫在了下方。可是對於右側第三個圖形，恐怕是遇上硬骨頭了，用盡渾身解數，怎麼試也不會成功。實際上這第三個圖形就是著名的“七橋問題”，七條線相當於七座橋，想一次性不重複地走完七座橋是不可能的。

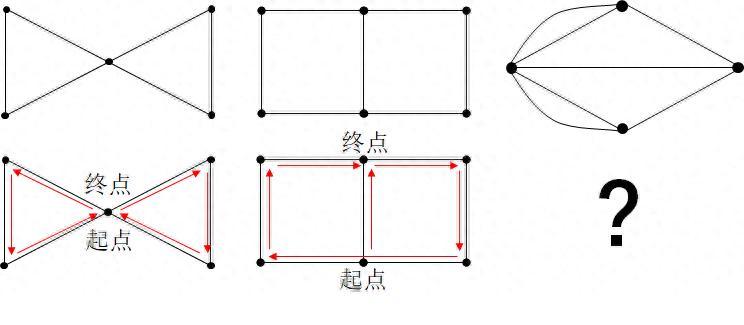
那麼什麼樣的圖形可以一筆畫出來，什麼樣的不能？奇偶數就是幕後的支配者。圖中如果某個節點連接的線條數爲奇數條，稱爲奇點；如果某個節點連接的線條數爲偶數條，稱爲偶點。一筆畫規律是：只有圖中具有0個或2個奇點的圖，纔可以一筆畫成。上面三個圖形中各個節點的線條數，以及屬於奇點還是偶點，在標註了之後（如下圖），就一目瞭然了。第一個“蝴蝶結”圖中有0個奇點，第二個“橫八字”圖中恰好有2個奇點，都滿足上述條件，可以一筆畫出來，而第三個圖中有多達4個奇點，自然不符合一筆畫的條件。

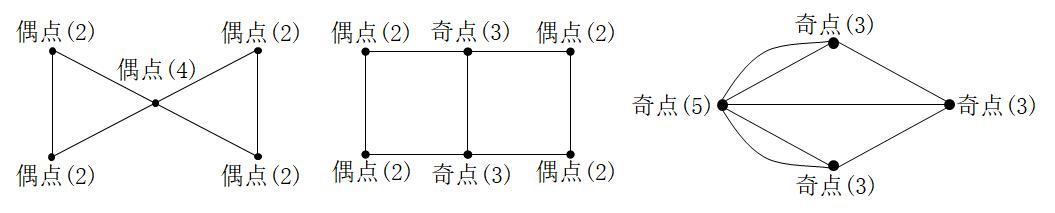
以上所說的規律又是怎麼得到的呢？在一筆畫的過程中，所有的節點可以分爲一個起點，一個終點，其它中途點這三類。中途點到達了一次之後，也必須離開一次，所以無論是“一面之交”，還是“多次拜訪的老朋友”，必須要是偶點，而起點允許有一次“一去不復返”，出發後就不再返回，終點允許有一次“落葉歸根”，到達後就不再出發，這樣起點和終點可以“破例”成爲2個奇點（如“橫八字”圖），但如果起點和終點是重合的，這一個點也會和其它中途點一樣成爲偶點，也就是0個奇點的情形（如“蝴蝶結”圖）。而像“七橋問題”中有四個節點全部是奇點，實在讓人勉爲其難，起點和終點怎麼樣也不需要有那麼多個，於是“七橋問題”成爲了無解的一筆畫難題。

現實中一筆畫不僅僅是個遊戲，還屬於計算機圖論專業研究範圍，在物流，運籌，交通，網絡通信，社交關係結構中都發揮重要作用，比如一個快遞小哥選擇怎樣最方便的路線，才能“不走回頭路”地送完所有郵件。

(a) (b)

(c) (d)

除了一筆畫之外，奇偶數還有一個更加神奇的本領，可以幫你“心靈感應”，讀出別人的心思，你相信嗎？我們從一個簡單的撲克牌魔術說起。魔術師首先把16張撲克牌正面朝上擺成一個陣列（如左上方圖a所示），其中9張是黑色，都擺在了一起，剩下7張是紅色，擺在了外圍一圈。接下來找三位觀衆上臺，在交代了每位觀衆需要做什麼之後，魔術師就背對大家，對於接下來發生的事情“毫不知情”。首先第一位觀衆選擇任意數量黑色牌翻過去，負責把黑色牌正面朝上還是背面朝上打亂（達到右上方圖b的效果），但規定不能動紅色牌。然後輪到第二位觀衆選擇任意數量紅色牌翻過去，負責把紅色牌正面朝上還是背面朝上打亂（達到左下方圖c的效果），但規定不能動黑色牌。最後第三位觀衆在所有的十六張牌中選一張，再翻一下，原本正面朝上就變成背面朝上，原本背面朝上就變成正面朝上（達到右下方圖d的效果，例如黑桃2被翻了）。此時魔術師再轉過身來，他說自己並沒有看到剛剛發生的一切，但憑藉第三位觀衆留下的蛛絲馬跡，就能猜出最後哪張牌被動過了，併成功指出是黑桃2.。

那麼魔術師是怎麼做到的呢？可以提示一下大家，三位觀衆中有一位是“托兒”，你能猜出來是哪位嗎？正確答案是第二位觀衆。而魔術師事先也僅僅和這位觀衆做了一個簡單的約定，就是儘管他只能翻紅色的牌，但要假裝隨意翻的，實際有意地保證每一行和每一列中正面朝上牌的個數都是奇數張（1張或3張），而不是偶數張，大家可以從左下方的圖裏再次確認下是不是這樣。之後第三位觀衆無論翻了16張中的哪一張，都會破壞奇數張的規律，造成某一行和某一列正面朝上牌的個數變爲偶數張，魔術師從這一行和列的交叉點位置就可以找出最後被動過的牌。

這同樣不僅僅是一個簡單的撲克牌魔術，在現在計算機，互聯網和通信中，各種信息都表示爲了大量的二進制的1和0數據，如果撲克牌正面朝上和背面朝上分別表示1和0，每張牌相當於一個比特，那麼9個比特的黑色牌可以表示實際要儲存或者傳輸的數據，7個比特的紅色牌相當於外加的校驗數據，通過這種“奇偶校驗”，當16個比特中任何一個出錯的時候（相當於被第三位觀衆翻過來的“誤碼”），接收方就可以檢測並糾正過來，整個過程稱爲“信息糾錯編碼”。當然奇偶校驗只是其中最簡單的一種方式，還有其它很多更加精巧設計的複雜信息糾錯編碼方式。

我們平時在超市購物所使用的條形碼，還有移動支付和社交小程序使用的二維碼，裏面的黑白線條或者黑白方塊就表示了大量的1和0，爲了應對掃碼讀碼時可能出現的錯誤，其中也都使用了信息糾錯編碼，一個二維碼不清晰了，扭曲變形了，甚至部分區域被一個頭像遮擋住，還是可以正確讀取信息。

奇偶數還可以用來表演另外一個魔術，下面左側和中間兩張”胡椒”的圖片，是不是看起來一模一樣，你能觀察到有任何的分別嗎？但詭異的是，左側胡椒圖片一切正常，無法提取出信息，中間胡椒圖片卻“另有乾坤”，可以從中提取出右側的密碼信息。這稱爲圖像信息隱藏（或隱寫），又是怎樣做到的呢？

在計算機上，每張照片或者圖像放大了之後，都會像馬賽克一樣，是由一個個小方塊組成的，每個小方塊稱爲一個像素。而單個像素的明暗程度或者顏色可以用數字來表示，比如在一張黑白照片（專業稱灰度照片）中，可以用0到255中間某個數字表示灰度深淺，0表示全黑色，255表示全白色，之間的數值則表示從黑色，深灰色，中灰色，淺灰色，一直到白色的逐漸過渡。如果兩個像素的灰度值只相差1，表示顏色非常接近，人眼實在難以分辨。而如果是彩色圖片，則要用三個數字表示一個像素，分別表示紅綠藍三原色的深淺。

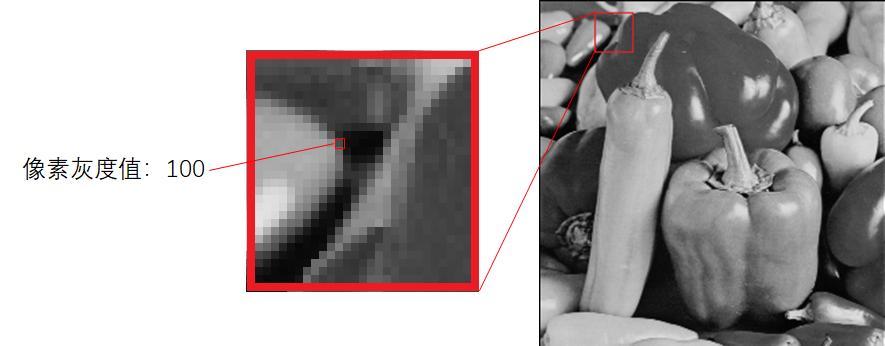
正常來說，每個像素的灰度值是奇數還是偶數是隨機的，碰巧決定的，如果人爲通過加1或者減1，把一些像素的灰度值做稍微更改，就可以讓奇數和偶數像素值的排列不再隨機和無意義，而是表示要隱藏的信息。如上所說，各種信息都可以用二進制的1和0表示，一個像素灰度值如果是奇數，就表示1，偶數就表示0，這樣每個像素可以表示一個隱藏的比特，一整張處理後的圖片就可以隱藏着大量信息，並且圖片本身發生的改動還微乎其微，很難察覺出來。

圖像信息隱藏在保密通信，版權保護，軍事情報，文件票據防僞等場景中有很多的應用。例如一位作者自己創作了一幅畫或者一段視頻作品，公開上傳後，被別人抄襲，結果臉皮厚的抄襲者還反過來聲稱作品是自己先創作的，真正作者纔是抄襲的一方，原作者如果事先在作品中把個人信息隱藏進去，就可以作爲證據，證明自己纔是真正的版權擁有者。而如果一份保密文件只能在十個人內部傳閱，不得泄露外傳，可以將分發給每個人的文件分別隱藏進不同信息作爲標記，當有人違反規定將文件外傳之後，可以根據外傳的文件中隱藏的信息判斷出誰是“內鬼”。

奇數和偶數看似簡單，卻又不簡單，通過巧妙的設計，可以在計算機圖論、信息編碼、圖像信息安全等各種任務中大顯身手，無所不能的表現簡直超乎想象。

作者：焦述銘 大灣區大學