在上一篇中，我們跟隨沃爾夫岡·泡利，從他的成長軌跡到“泡利不相容原理”的提出，見證了這位天才物理學家是如何爲原子內部的電子排布建立起不可動搖的基本規則。但在科學史的長河中，這只是他傳奇故事的開端。

舊量子理論的困境和新理論的迫切性

20世紀20年代後期，物理學正處在劇烈的思想轉型期。舊量子論在解釋氫原子光譜等簡單問題時曾立下功勞，但面對更復雜的多電子原子、分子結構以及輻射與物質相互作用時，它顯得捉襟見肘。科學界迫切需要一種新的理論框架來接替它。

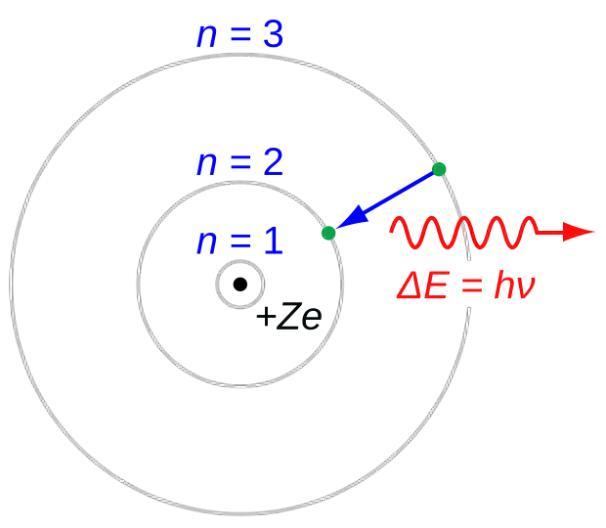
氫原子（Z = 1）或類氫原子（Z > 1）的玻爾模型示意圖

（圖片來源：Wikipedia）

在這一背景下，兩種全新的理論幾乎同時登上舞臺——矩陣力學與波動力學。它們在數學形式和物理直覺上截然不同，卻在計算結果上驚人一致。這一現象引發了學術界的分歧：支持矩陣力學的一方和推崇波動力學的一方在會議、論文甚至私人通信中展開了激烈爭論。有人說，那是量子力學黎明時分的“東西方陣營對峙”——一邊是抽象的代數矩陣，一邊是直觀的波動方程。

泡利正是在這樣一個理論分裂的關鍵時期發揮了重要作用。他不僅是兩大陣營都尊重的學術權威，更是極少數能夠跨越兩種理論壁壘的人。與此同時，他還在粒子物理學的早期困境中提出了震撼性的預言——中微子假說。這一系列貢獻，使得泡利從“泡利不相容原理的發現者”成長爲“量子秩序的構建者”，併成爲那個年代的思想中堅。

分立發展的早期量子力學

1925年夏天，年輕的海森堡因花粉過敏前往北海的赫爾戈蘭島療養。在這個幾乎與世隔絕的小島上，他得以遠離日常的學術紛擾，專注思考一個困擾物理學家的根本問題：既然電子軌道無法直接觀測，不如干脆放棄軌道的概念，只用可測量的物理量來建立理論——比如光譜線的頻率和強度。

這一思路可謂石破天驚。海森堡將原子中電子躍遷產生的光譜數據整理成表格，並嘗試用這些表格直接進行計算。在推導過程中，他意外發現這些量的運算規律並不遵循普通的乘法交換律，而是一種全新的“非交換”代數。這種奇特的數學結構很快引起了玻恩和約當的興趣，他們與海森堡合作，將這一想法形式化爲矩陣力學，並在1926年發表了奠基論文。

矩陣力學的數學形式高度抽象——物理量用矩陣表示，時間演化由矩陣方程支配，測量結果與矩陣的特徵值直接相關。在這種理論裏，經典物理中的核心量（如位置和動量）不再能隨意交換順序運算，這種“不對易性”成爲量子理論的基本特徵之一。雖然這種理論在描述微觀現象時非常精確，但缺乏直觀圖像，讓許多物理學家難以理解。

與此同時，1926年1月，瑞士蘇黎世大學的薛定諤受德布羅意“物質波”假設啓發，提出了另一種完全不同的理論——波動力學。他認爲電子應被視作一種波，並建立了著名的薛定諤方程來刻畫電子的時間與空間演化。與矩陣力學的抽象不同，波動力學提供了可視化的物理圖景：電子狀態對應波函數，可以像水波在湖面上傳播那樣直觀地描繪。

最初，很多人以爲這兩種理論必有一真一假。然而，當薛定諤計算氫原子的能級時，他驚訝地發現與矩陣力學的結果完全一致。這種數學上一致、形式上迥異的局面，使物理學界一時間陷入兩派論戰：矩陣力學派稱波動力學“缺乏嚴謹性”，波動力學派則批評矩陣力學“晦澀反直覺”。有學者回憶，在1927年的索爾維會議上，兩個陣營的討論有時激烈到幾乎變成辯論賽。

就像有人用文字描述蘋果，有人用圖畫描述蘋果，雖然方法不同，但表示的其實是同一個物體。泡利此時展現出少有的冷靜與寬廣視野。他早期支持海森堡的矩陣力學，同時也欣賞薛定諤波動力學的數學優雅。作爲兩派都信任的物理學家，他開始嘗試尋找它們之間的內在聯繫。

索爾維會議第五次會議（1927年）

（圖片來源：Wikipedia）

泡利統一量子力學框架——一枚硬幣的兩面

泡利的數學功底和物理直覺，使他成爲理解這場理論分裂的最佳人選。1926年，他抓住了關鍵：在波動力學中描述電子狀態的“波函數”，如果按能量本徵態展開，這些展開係數剛好對應着矩陣力學中的矩陣元。通過這一對應關係，泡利證明了兩種理論的等價性。這就像證明了“文字描述的蘋果”和“圖畫描述的蘋果”其實是同一個蘋果。泡利用簡單的數學推導，證明了兩種理論其實是等價的——它們只是從不同角度描述了同一個微觀世界。

值得注意的是，薛定諤也在同年發表的第四篇波動力學論文中獨立完成了等價性的嚴格證明。但泡利的信件在學界流傳甚廣，他在信中以極簡潔的數學推導和清晰的物理解釋，打消了不少人對矩陣力學和波動力學之間矛盾的疑慮。這種橋樑式的貢獻，爲量子力學的統一奠定了基礎。

1927年，泡利在研究電子自旋理論時引入了三組特殊的二維矩陣——後來被稱爲“泡利矩陣”。它們簡潔地描述了自旋 1/2 粒子（如電子、質子、中子）在空間各方向上的投影性質。今天，泡利矩陣不僅是量子力學教材的必備內容，更在覈磁共振成像、量子通信、量子計算機的邏輯門設計等領域廣泛應用。比如，在量子計算中，泡利矩陣對應的 X、Y、Z 操作構成了最基本的單量子比特邏輯門，是實現任意量子算法的基石。

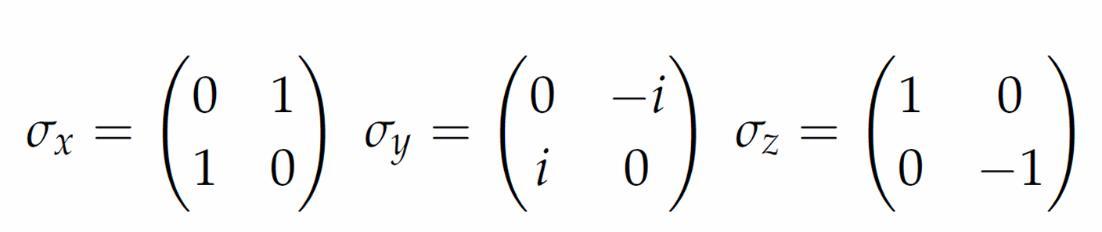
泡利矩陣（X、Y、Z）

（圖片來源：Wikipedia）

進入1930年代，泡利與韋斯科普夫等人合作，探討場量子化和理論中的發散問題。他們的分析雖未立即解決無窮大難題，但爲後來的重整化方法提供了思想基礎。與此同時，泡利敏銳地察覺到自旋與粒子統計性質之間存在深刻聯繫，並在1940年完成了“自旋–統計定理”的嚴格證明——自旋爲半整數的粒子必須服從費米–狄拉克統計，而自旋爲整數的粒子則遵循玻色–愛因斯坦統計。這一定理後來成爲量子場論和粒子物理的支柱之一。

中微子的預言——尋找能量的“幽靈”

1920年代末，核物理學家在研究β衰變時發現了一個令人困惑的現象：放射性原子核衰變時會放出電子，但電子帶走的能量總是“不夠”——按照能量守恆定律，反應前後的能量應該一樣，但實際測量時，總有一部分能量“消失”了。如果β衰變只涉及原子核和電子，那麼能量守恆要求電子應帶走一個確定能量。這似乎暗示——能量守恆在微觀世界被破壞了。

1930年12月4日，沃爾夫岡·泡利（Wolfgang Pauli）給“親愛的放射性女士們先生們”寫了一封著名的信，提出了大膽假設：除了電子外，β衰變還會產生一種當時未知的中性粒子，質量極輕，幾乎不與物質作用，但能帶走缺失的能量和動量。在信件的開頭，泡利甚至半開玩笑地稱自己是“提出無法被探測到粒子的瘋子”，但這份自嘲並未掩蓋他對守恆定律的堅定信念。

1930年12月，沃爾夫岡·泡利給“親愛的放射性女士們先生們”寫了一封著名的信件。

（圖片來源：Wikipedia）

1932年，查德威克發現了中子。同年，費米在構建β衰變理論時，爲避免與中子混淆，創造了“neutrino（中微子）”一詞，並在1934年的理論中將其納入弱相互作用框架，成功解釋了電子能譜的連續性。

然而，中微子與物質的相互作用截面極小，使其探測極爲困難——它能輕鬆穿過地球，就像穿過空氣一樣。直到1956年，弗雷德·雷恩斯（Fred Reines）和克萊德·考恩（Clyde Cowan）利用核反應堆產生的大量反中微子，纔在實驗中首次直接探測到這一粒子，驗證了泡利26年前的預言。賴因斯後來因中微子探測獲諾貝爾獎，而泡利已於1958年病逝，未能親眼見證這一成果。

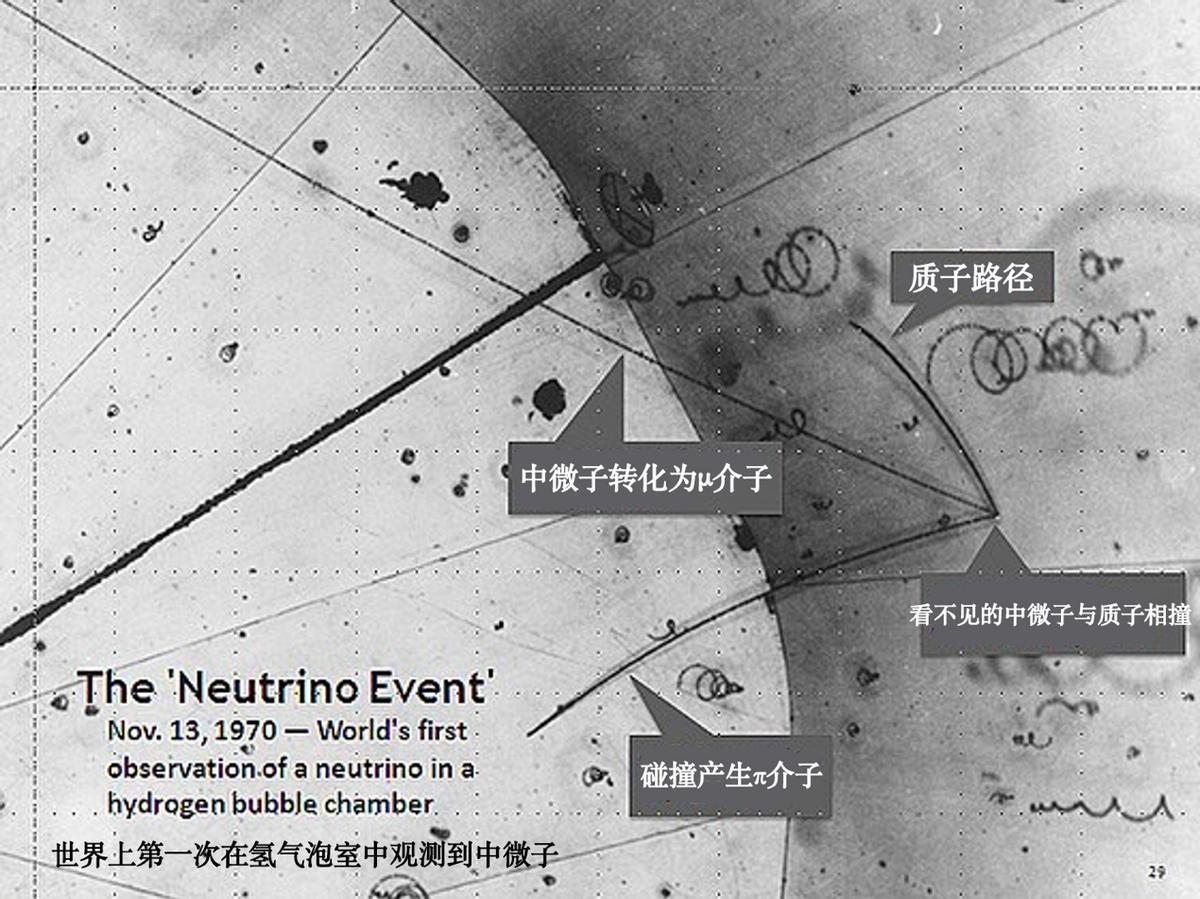
1970年11月13日，弗雷德·雷恩斯（Fred Reines）和克萊德·考恩（Clyde Cowan）在阿貢國家實驗室首次使用氫氣泡室探測中微子。其中，中微子撞擊氫原子中的質子，碰撞發生在照片右側發出三條軌道的點。

（圖片來源：Wikipedia）

泡利的中微子假說，不僅解決了β衰變的能量難題，更體現了他科學思維的特質：寧可引入一種極難驗證的新粒子，也不放棄能量守恆這一物理學基石。這種既嚴守原則又敢於創新的精神，使他在科學史上獨樹一幟。

結語——量子秩序的構建者

從統一矩陣力學與波動力學，到引入自旋的數學語言，再到預言中微子，泡利在“不相容原理”之後的十年間，爲量子力學的發展奠定了結構性和基礎性的支撐。他不僅解決了當時懸而未決的理論難題，更在原則與方法論上爲後來的物理學家設定了高標準，確保了量子理論的穩定與延展。

1958年，沃爾夫岡·泡利安葬於佐利孔公墓。

（圖片來源：Wikipedia）

如果說“泡利不相容原理”是量子世界的基本法則，那麼泡利在1926年至1934年間的工作，就是爲這部憲法制定法律、確立司法和執行機制的人。他在理論紛爭中保持冷靜，在實驗困境前堅持守恆定律，用邏輯的嚴謹和想象的勇氣，讓量子力學從初生走向成熟。這種科學家的“制度設計”能力，使他不僅是發現者，更是守護者。

今天，當我們在量子計算機中調用泡利矩陣構建量子邏輯門，或在天體物理實驗中追蹤中微子信號時，依然能感受到這位大師留下的思想力量。沃爾夫岡・泡利的名字，早已鐫刻在量子物理的基石之上。

參考文獻：

[1] Born M, Heisenberg W, Jordan P. Zur quantenmechanik. II[J]. Zeitschrift für Physik, 1926, 35(8): 557-615.

[2] Schrödinger E. Quantisierung als eigenwertproblem[J]. Annalen der physik, 1926, 385(13): 437-490.

[3] Pauli Jr W. Zur quantenmechanik des magnetischen elektrons[J]. Zeitschrift für Physik, 1927, 43(9): 601-623.

[4] Pauli W. Letter to the physical society of tubingen[J]. Reproduced in [2], 1930.

[5] Fermi E. An attempt of a theory of beta radiation. 1[J]. Z. phys, 1934, 88(161): 19.

[6] Bethe H, Peierls R. The “neutrino”[J]. Nature, 1934, 133(3362): 532-532.

出品：科普中國

作者：欒春陽 王雨桐（清華大學物理系博士）

監製：中國科普博覽