你有沒有想過，爲什麼我們身邊的物質能保持穩定？石頭不會突然消散，水也不會無緣無故變成其他物質——這背後，是微觀世界的電子正遵循着一套嚴格的“秩序規則”。

想象一下，如果原子世界沒有規則，電子們可以隨意擠在同一個位置、擁有完全相同的狀態，我們的宇宙將會怎樣？元素週期表將不復存在，化學反應會陷入混亂，構成我們世界的一切物質都將崩潰。

20世紀初，一位年輕物理學家爲原子世界立下了一條看似簡單卻至關重要的鐵律——泡利不相容原理。它不僅解開了困擾科學界多年的謎題，更奠定了理解物質世界的基礎。這位物理學家，就是以其超凡洞察力和近乎苛刻的嚴謹性著稱的沃爾夫岡·泡利（Wolfgang Pauli）——量子物理領域當之無愧的“秩序守護者”。

微觀世界的混亂難題

20世紀初的物理學，正站在一場顛覆性革命的門檻上。曾經輝煌的經典力學和電磁學，面對原子內部的微觀世界時，顯得力不從心。原子光譜的神祕規律、元素週期表背後的結構之謎，特別是磁場中原子譜線那令人困惑的“反常”分裂現象，都在不斷推動物理學家們向未知的領域進發。

在這片充滿挑戰的科學海洋中，沃爾夫岡·泡利憑藉其獨特的個性和銳利的洞察力嶄露頭角。他不僅擁有卓越的數學天賦，更懷揣着一種近乎苛刻的科學直覺——對理論邏輯一致性的追求達到了“吹毛求疵”的地步，以至於同行們稱他爲“量子力學的良心”。而他的名字，最終因一條簡潔而深刻的規則響徹物理學界——泡利不相容原理。

青年時期的沃爾夫岡·泡利（1924年）

（圖片來源：Wikipedia）

然而，泡利成名的起點並非直接提出那條著名的“泡利不相容原理”，而是源於一個讓物理學家們頭痛了數十年的難題——反常塞曼效應。

光譜謎案——塞曼效應的反常挑戰

1896年，荷蘭物理學家彼得·塞曼（Pieter Zeeman）發現了一個奇妙現象：當發光的原子氣體被置於強磁場中時，其發出的光譜線會發生分裂。這便是著名的“塞曼效應”，它在1902年爲塞曼和洛倫茲贏得了諾貝爾物理學獎。這種現象在氫原子這樣的簡單體系中很有規律，譜線分裂得整齊對稱，被稱爲“正常塞曼效應”。經典電子軌道理論和早期的量子論可以解釋它：磁場改變了電子軌道運動的能量，導致能級分裂。

然而，隨着光譜儀精度的提升，科學家們在更復雜的原子（尤其是多電子原子）中觀察到了截然不同的景象：譜線分裂的模式既不整齊也不對稱，間距也毫無規律可循。這便是令人棘手的“反常塞曼效應”。它在實驗上被反覆證實，但當時的理論完全無法解釋該現象，無論是經典理論還是玻爾的原子模型，讓物理學家們對此束手無策。

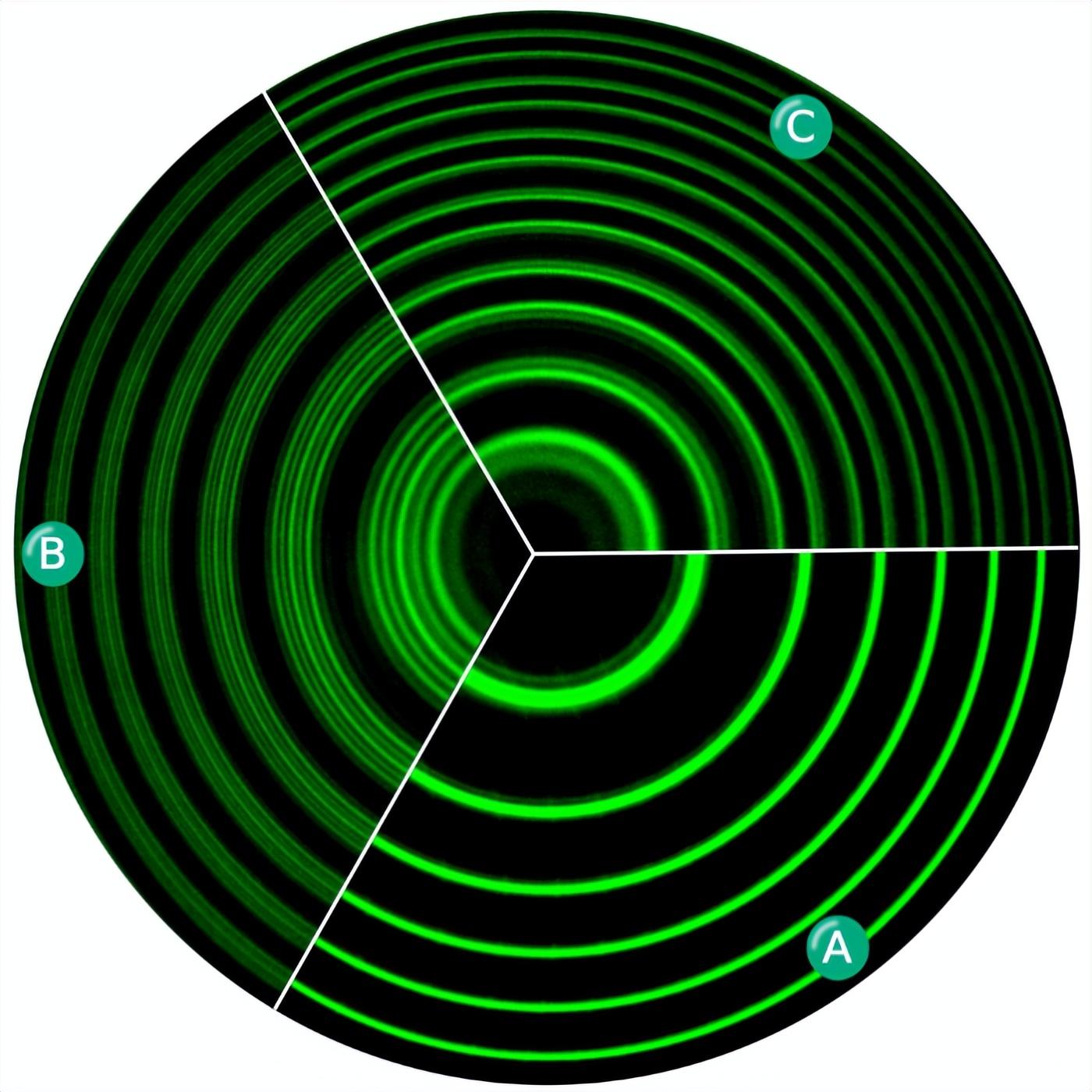
汞蒸氣燈在546.1 nm波長處的光譜線顯示出反常塞曼效應。(A) 沒有磁場。(B-C) 在磁場作用下，譜線分裂爲橫向和縱向塞曼效應。

（圖片來源：Wikipedia）

爲了“修補”理論，科學家們嘗試了各種辦法。20世紀10至20年代初，德國物理學家阿爾弗雷德·朗德（Alfred Landé）提出了一個經驗性的解決方案——引入神祕的g因子。這個因子成功地將分裂模式與原子角動量、磁矩聯繫起來，公式計算與實驗數據吻合得不錯。但問題在於：g因子究竟是什麼？它的物理來源是什麼？朗德公式更像是一個精妙的數學“補丁”，並未觸及現象的核心根源。

進入20世紀20年代，物理學界迫切需要一種全新的思路，來揭開反常塞曼效應的微觀機制之謎。年輕的泡利，正是在這個關鍵問題上展現了他非凡的洞察力。

破解謎題——從反常塞曼效應到“泡利不相容原理”

沃爾夫岡·泡利於1900年出生在維也納，自幼便展現出非凡的學術潛力。化學家父親和熱愛文藝的母親，讓他從小在理性科學與人文思想的交融環境中成長。18歲進入慕尼黑大學，師從原子物理學大師阿諾德·索末菲後，他迅速成爲理論物理界一顆耀眼的年輕新星。

1921年，年僅21歲的泡利發表了一篇長達250頁的綜述論文，系統總結了相對論與電子理論的成果。這篇論文至今仍被視爲狹義相對論的權威文獻之一。這份工作不僅讓他在物理學界聲名鵲起，更充分展現了他駕馭複雜理論問題的卓越能力。也正是在此期間，他將目光投向了那個令人困惑的難題——反常塞曼效應。

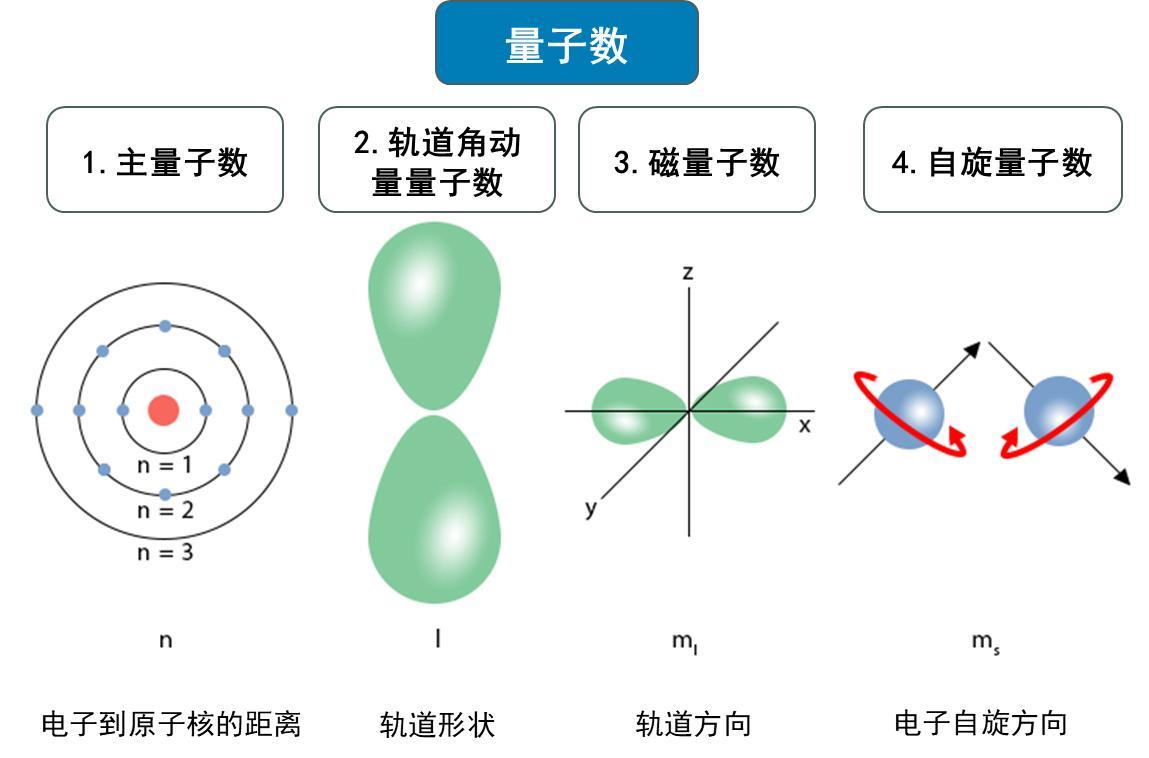
面對反常塞曼效應這個難題，泡利敏銳地意識到，問題的癥結在於當時對電子狀態的描述不夠完整。根據舊量子論，一個電子的狀態由三個量子數（可以理解爲電子的“身份證號碼”）描述：

1. 主量子數n（Principal Quantum Number，決定主要能級，也就是電子離原子核的遠近）；

2. 軌道角動量量子數l（Azimuthal Quantum Number，決定軌道形狀，如圓形、橢圓）；

3. 磁量子數m（Magnetic Quantum Number，決定軌道空間方向）。

然而，實驗數據清晰地表明：即使這三個量子數完全相同，電子仍然可能表現出不同的能量和磁性質。這意味着，電子一定還隱藏着第四個自由度！

1925年，泡利做出了一個革命性的假設：電子除了n、l、m之外，還必須擁有一個只能取兩個不同值的量子數。這個神祕的第四個量子數可以完美解釋g因子的來源，並精確復現反常塞曼效應中那複雜的分裂模式。儘管泡利當時尚不清楚這個量子數的具體物理含義，但他憑藉嚴密的數學推導堅信它的存在。

四個量子數的示意圖

（圖片來源：Wikipedia）

同年，泡利更進一步，提出了那項影響深遠的原理：泡利不相容原理（Pauli Exclusion Principle）。其核心內容是：在一個原子中，不可能有兩個（或更多）電子具有完全相同的四個量子數。簡單來說，這條原理表達的意思是：在同一個原子中，不可能有兩個（或更多）電子的四位“身份號碼”完全相同。這意味着，每一個特定的量子態，最多隻能容納一個電子。如果將“量子態”比做房間，也就是每一個電子都必須遵守“單身公寓”法則。如果考慮到第四個量子數（後來被證明是電子的“自旋”）只有兩個取值，那麼每個原子軌道（由n、l、m定義）最多可以容納兩個電子，且它們的自旋方向必須相反（一個“上旋”，一個“下旋”）。

這個看似簡單的物理法則，瞬間解決了多電子原子光譜規律的謎團，並從根本上解釋了元素週期律的成因：當原子的最外層電子殼層被電子按照不相容原理和能量最低原理填滿時，原子就變得非常穩定，呈現出惰性氣體的化學性質；而當外層殼層未填滿時，原子就容易與其他原子相互作用，形成化學鍵，表現出特定的化學活性。

泡利不相容原理的提出，是原子理論的一次質的飛躍。它不僅破解了光譜學上的關鍵難題，更爲即將到來的量子力學革命——矩陣力學和波動力學的誕生與發展——奠定了不可或缺的基礎。

自旋與量子世界的秩序法則

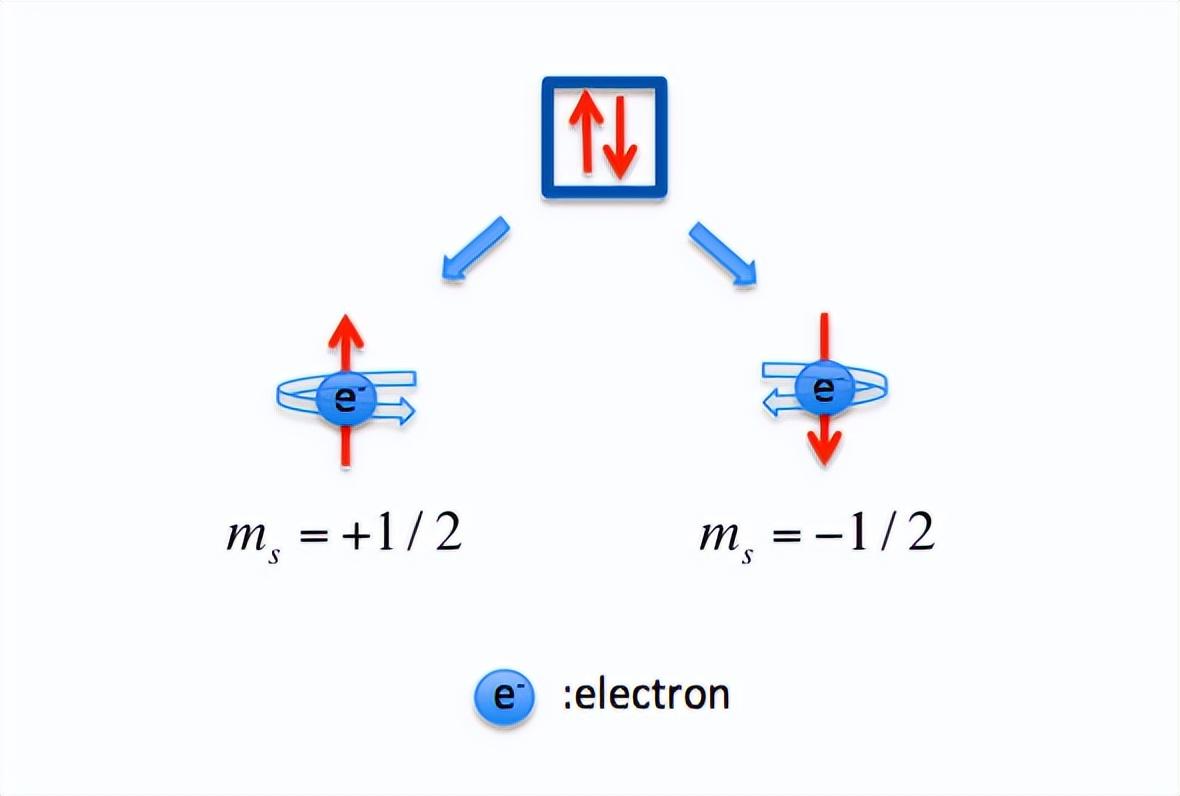
就在泡利提出第四個二值量子數的同年下半年（1925年），萊頓大學的喬治·烏倫貝克（George Uhlenbeck）與薩繆爾·古德斯密特（Samuel Goudsmit）勇敢地提出了電子自旋（Electron Spin）的概念。他們認爲電子具有一種內稟（粒子的自帶特徵，與外界條件無關）的角動量，如同在繞自身軸旋轉（儘管這個經典圖像不完全準確），其投影值只能取（上旋）或（下旋）。這爲泡利假設的第四個量子數提供了清晰而具體的物理解釋。

雖然泡利最初對“電子像小球一樣自轉”的直觀圖像表示懷疑（因爲經典自旋模型與相對論矛盾），但他很快接受了自旋作爲一種內稟量子自由度的數學形式，並在量子力學的發展中被廣泛運用。1927年，他系統地表述了兩分量自旋波函數，並引入了著名的泡利矩陣（Pauli Matrices）來描述自旋算符，以及將自旋磁矩效應納入薛定諤方程的泡利方程（Pauli Equation），這些工具迅速成爲處理自旋問題的標準武器。

電子“自旋”的示意圖

（圖片來源：Wikipedia）

自旋概念的引入不僅完美詮釋了泡利不相容原理的物理圖景（即同軌道兩個電子必須自旋相反），更將這條原理提升到了更深層次的物理規律。

1926年，恩里科·費米（Enrico Fermi）與保羅·狄拉克（Paul Dirac）各自獨立地建立了費米-狄拉克統計（Fermi-Dirac Statistics）：具有半整數自旋（如1/2，3/2…）的粒子（稱爲費米子，如電子、質子、中子）必須遵守泡利不相容原理，每個量子態最多隻能容納一個粒子；而具有整數自旋（0，1，2…）的粒子（稱爲玻色子，如光子、介子）則不受此限制，它們服從玻色-愛因斯坦統計（Bose-Einstein Statistics），可以大量聚集在同一個量子態上（如激光就是大量光子聚集在同一狀態形成的）。

在量子場論的發展中，泡利進一步將這一統計法則昇華爲一個深刻的物理定理：1940年，他首次給出了自旋-統計定理（Spin-Statistics Theorem）的嚴格證明，在相對論性量子場論的框架下，將“不相容”的特性（表現爲反對易關係）與粒子的半整數自旋不可分割地聯繫在了一起。

結語：秩序的基石

泡利不相容原理誕生於對原子光譜的探索，但其影響早已超越了原子物理的範疇，成爲我們理解整個物質世界基本秩序的一塊基石。從解釋化學元素的週期性排列，再到決定固體中電子形成的能帶結構（是導體、半導體還是絕緣體的關鍵），它的身影無處不在。

然而，揭示原子世界的物理法則，僅僅是泡利輝煌科學旅程的起點。在接下來的歲月裏，這位“量子秩序的守護者”將繼續發揮關鍵作用：他深度參與了量子力學兩種數學表述（海森堡的矩陣力學與薛定諤的波動力學）統一的證明工作；更在粒子物理面臨能量守恆危機的“至暗時刻”，大膽預言了中微子（Neutrino）的存在——這個幽靈般的粒子最終在1956年被實驗直接探測到，再次印證了他驚人的物理直覺。

在下一篇文章中，我們將跟隨泡利的腳步，看他如何從原子電子的排布規則出發，邁向構建量子理論的宏偉殿堂，並在其中留下不可磨滅的印記。

參考文獻：

[1] Pauli W. Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren[J]. Zeitschrift für Physik, 1925, 31(1): 765-783.

[2] Zeeman P. The effect of magnetisation on the nature of light emitted by a substance[J]. nature, 1897, 55(1424): 347.

[3] Uhlenbeck G E, Goudsmit S. Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons[J]. Die Naturwissenschaften, 1925, 13(47): 953-954.

[4] Dirac P A M. On the theory of quantum mechanics[J]. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 1926, 112(762): 661-677.

[5] The Nobel Prize in Physics 1945 was awarded to Wolfgang Pauli "for the discovery of the Exclusion Principle, also called the Pauli Principle"

出品：科普中國

作者：欒春陽 王雨桐（清華大學物理系博士）

監製：中國科普博覽