在聊到數學這一領域的時候，或許所有人都會聽過這樣一個定律，那就是平行線，永不相交。

古往今來，這條定律一直都是國際數學界雷打不動的金科玉律，無數個數學成就也都建立在這一定律之上。

可俄羅斯有一個人，卻不相信這個邪，他花了一輩子的時間，想要證明平行線是可以相交的。

（平行線，永不相交）

可是等他真的完成了這一切以後，他卻從“聲名斐然的學者”淪爲 “招搖撞騙的神棍”；不僅遭受了普通民衆嘲諷，衆多傑出數學家也對他冷嘲熱諷。

學術上，他的論文無法發表，遭到所有人的排擠；事業上，被教育部剝奪熱愛的教學工作；生活中，大兒子患病去世，多重打擊下他雙目失明，最終鬱鬱而終。

結果他含冤去世12年以後，所有人又說他是對的，這個人就是俄羅斯奇才數學家羅巴切夫斯基，他用他的悲慘一生，告訴了全世界，只要你手中掌握着真理，哪怕是千夫所指，時間也會證明你的正確。

（羅巴切夫斯基）

超級天才，俄羅斯的梅貽琦

羅巴切夫斯基的一生，或許就是天才的代名詞。

他出生於1792年12月1日，年少天才非凡。15歲就進入了俄羅斯首屈一指的名校喀山大學當中學習，4年後獲物理數學碩士學位並留校任教，堪稱絕對的“年少得志”。

24歲時，在其他同齡人可能還是學生的時候，他就已經成爲了喀山大學的副教授，成爲了彼時學界有名的當紅炸子雞；30歲，當其他人還在爲房貸花唄而發愁時，羅巴切夫斯基發表了多篇關於數論、幾何的論文，其中多篇被評爲當年俄國數學界的標杆之作。

（喀山大學）

35歲時，他更是憑藉自己多年來兢兢業業的工作，成爲了喀山大學歷史上最年輕的大學校長之一。

當校長期間，他兩次力挽狂瀾，將喀山大學從重大災情的泥沼中拯救出來；大力引進優秀人才，修建教學樓、圖書館、天文臺等基礎設施，爲學校的發展奠定堅實基礎。

可以說，彼時的他之於喀山大學，就相當於梅貽琦蔡元培之於清華北大。

而真正讓這位喀山大學校長，坐實“俄羅斯梅貽琦”之稱謂的，當屬他那令人驚歎的教育天賦。他曾撰寫出多部有關教學法的著作，極大推動了彼時俄羅斯的教育工程方向。

日後喀山大學能夠培養出列夫·托爾斯泰和列寧這樣的優秀校友，羅巴切夫斯基功不可沒。

可以說，這樣的一個人，無論站在什麼樣的立場，用何等的眼光審視，都是當之無愧的學術巨擘，前途無可限量。如果不是他硬要和歐幾里得較勁的話，他的人生，遠比真實的歷史更加精彩。

（喀山大學天文臺）

和前輩死磕，推翻數學界的金科玉律

改變了羅巴切夫斯基命運的，其實是歐幾里得的第五公設問題。

歐幾里得第五公設問題堪稱數學史上最爲古老且著名的難題之一。公元前3世紀，古希臘著名學者歐幾里得在其人類數學史上最重要的著作《幾何原本》中提出了五個公設。

其中第五公設“若一條直線與另外兩條直線相交，所形成的兩個同旁內角之和小於兩直角，那麼當把這兩條直線無限延長時，它們必然會在這兩個內角所在的一側相交”，幾千年來，難倒了無數的學者大家，一度被人認爲是無解的存在。

（歐幾里得）

直到羅巴切夫斯基出現，這個問題纔得到瞭解決。原來前人的失敗或許並非能力不足，而是方向錯了，因爲此題根本無法被證明。

爲了驗證這個猜想，他採用了反證法：假設“過平面上直線外一點，至少可以作出兩條直線與已知直線不相交”，然後以此爲基礎推導幾何體系。令人意外的是，這套看似“荒謬”的假設，竟然推導出了一個邏輯自洽、毫無矛盾的新幾何體系。

更顛覆認知的是，在這個體系裏，原本相互平行的兩條直線，最終竟會相交；三角形的內角和也不再恆定爲 180°，而是小於此值。並且，不存在大小相異的相似三角形，僅存在能夠完全重合的“全同三角形”。

命途多舛的人生

1826年，羅巴切夫斯基在喀山大學的學術會議上公佈了自己的研究成果。可他的話音剛落，會場就陷入了一片譁然。在當時的數學家看來，這套理論簡直是“離經叛道”，是對傳統幾何學的褻瀆。有人當場嘲諷他 “異想天開”，有人私下裏稱他是 “胡說八道”，甚至連他的同事都對他避之不及。

面對鋪天蓋地的質疑和謾罵，羅巴切夫斯基沒有退縮。他一次次在學術期刊上發表論文，一次次在公開場合宣講自己的觀點。

可他的堅持，換來的卻是更殘酷的打壓：學術期刊拒絕刊登他的文章，教育部剝奪了他的教學資格，連曾經支持他的學校也與他劃清界限。

屋漏偏逢連夜雨，事業上的打擊還未平息，生活的苦難又接踵而至。他的大兒子患上重病，儘管他傾家蕩產求醫問藥，最終還是沒能留住孩子的生命。白髮人送黑髮人的痛苦，加上長期的精神壓力，讓羅巴切夫斯基的身體迅速垮掉，視力也逐漸衰退，最終徹底失明。

1856年2月24日，這位孤獨的數學先驅在抑鬱和絕望中離世，直到生命的最後一刻，他的理論也沒能得到世人的認可。

遲到的正名

1868年，在羅巴切夫斯基與世長辭後的第十二個年頭，他終於等來了遲到的肯定。

這一年，意大利著名學者貝爾特拉米藉助微分幾何的最新研究成果，證實了羅巴切夫斯基的理論並不是“空中樓閣”，而是能夠在現實模型中尋得與之對應模型的實例。

1871年，德國數學家克萊因更進一步，運用射影幾何的方法，構建了羅氏幾何的平面模型，從而徹底證明了這套幾何體系具有“無矛盾性”。

至此，“羅氏幾何”終於獲得了學界的廣泛認可。非歐幾何也從往昔被視爲的“異端學說”，搖身一變成爲了幾何學領域的重要分支。只可惜，這所有的榮譽，他已永遠無法親眼目睹了。

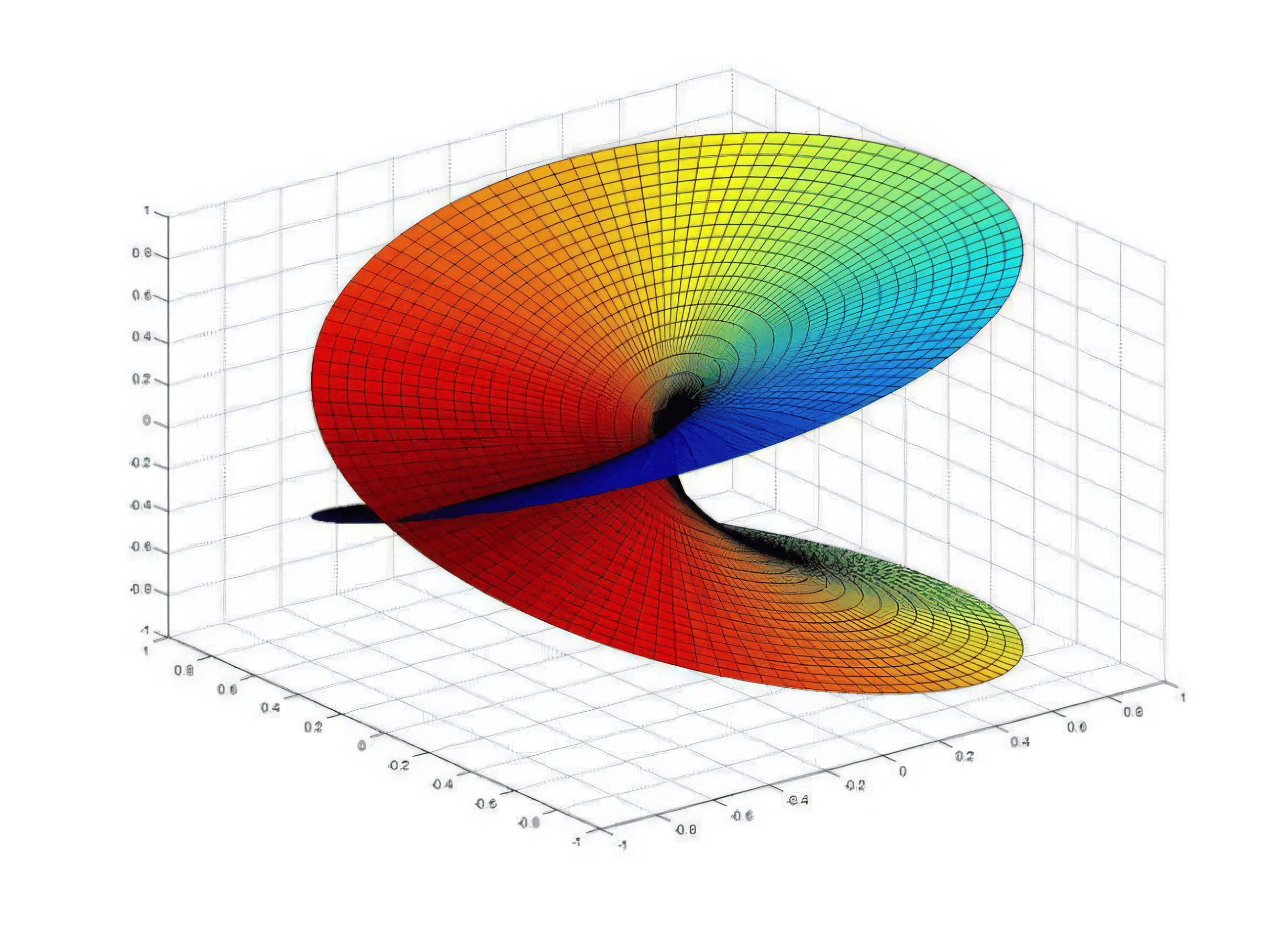
（羅氏幾何）

參考資料：

1、中國科學院《突破傳統的艱難探索：幾何學的革命者羅巴切夫斯基》