要揭開黑洞的神祕面紗，我們必須先理解愛因斯坦的廣義相對論，而它的核心，正是“時空彎曲”。別擔心，我不會用複雜的公式嚇跑你。今天，就讓我們從一場改變物理學的夢開始，一步步走進這個彎曲而迷人的宇宙圖景……

光速不變的頓悟時刻

要真正理解什麼是黑洞，就必須要理解什麼是廣義相對論，而要理解廣義相對論又要先理解什麼是時空彎曲，要理解時空彎曲，又要先理解狹義相對論。真的是一環扣一環，一個也繞不開。所以，今天這期節目，我不得不先從狹義相對論開始講起。當然，我是用最快速最簡單的方式帶你瞭解一下什麼是狹義相對論，我只講結論，不講推導過程。如果你對狹義相對論的推導過程感興趣，可以去聽我的另外一個專輯《時間的形狀》。

1905 年的某一天，在瑞士伯爾尼的專利局，26 歲的小專利員愛因斯坦正在椅子上打盹，他夢見自己正在黑黢黢的太空中飛行，速度跟光一樣快。這時候，他飛過一盞燈，這盞燈在他飛過的剎那間亮了起來。愛因斯坦猛的一下驚醒了，腦子中還在回憶着剛纔夢中的那盞燈。他突然問自己一個問題：如果我跑得跟光一樣快，我會看到什麼呢？難道會是一束靜止的光嗎？

我現在想問問我親愛的科友，你覺得愛因斯坦應該看到怎樣的景象？如果這個問題改爲，假如你跑得跟子彈一樣快，你經過一把槍，槍在你經過的同時射出子彈，請問，你能不能輕易地抓住出膛的子彈呢？我相信你一定會毫不猶豫地回答我：能！沒錯，如果是子彈，這個答案是毋庸置疑的，並且可以被實驗完全加以證實。

但是，光和子彈是一樣的嗎？

圖源：電影《尋祕自然：時間的形狀》

這個問題是讓愛因斯坦突然頓悟的關鍵問題。他經過一番仔細的思考，這裏我略過他的思考過程，只講愛因斯坦最後的思考結果。愛因斯坦認爲，哪怕自己跑得和光一樣快，自己也不可能看到一束靜止的光，不管自己相對於光源的運動速度有多快，自己始終會看到光以永恆不變的約 30 萬千米/秒的速度遠離自己而去。

這就是愛因斯坦在 1905 年做出的著名假設：光速不變。這個假設是說，光速是宇宙中的永恆速度，不管相對於任何物體，不管這個物體的運動速度有多快，光的相對速度都是永恆不變的。

圖源：電影《尋祕自然：時間的形狀》

我在這裏把光速不變叫做假設，而你可能看到在其他一些書上，它被稱爲光速不變原理。實際上，我想告訴大家，在物理學中，其實，所有的原理都是一種假設。xx 原理就等於 xx 假設。一個無比悲哀的事實是，從邏輯上來說，像光速不變這樣的假設它只能被推翻，卻不可能被完全證明。不論我們怎麼做實驗，我們都無法證明，超光速是肯定不存在的。我們最多隻知道，所有的實驗都表明，光速是我們能測量到的最快速度。

如果你天生邏輯感強的話，我估計你馬上就理解了我剛纔說的話，當然，你有可能要花很久才能想通，不要緊，我跟你一樣，也是花了很久很久纔想通這個邏輯。

所以，我想告訴大家。在物理學中，所有的原理和定律都是假設，或者用更通俗的話來說，它更像是物理學家們共同遵守的一種約定，也可以說成是一種信念，只能被證僞無法被完全證實。

相對論：時空一體化的革命

就是在光速不變這條最基本的假設上，愛因斯坦建立起了整個狹義相對論的理論大廈。那什麼是狹義相對論呢？如果用最常見也是最簡單的理解是四個字：鐘慢尺縮。就是說，一個運動的時鐘，在觀察者眼中，會變慢；一把運動的尺子，在觀察者眼中，它在運動方向上會發生收縮。請注意“在觀察者眼中”這幾個字，狹義相對論是一種觀察者效應。

在狹義相對論中，還有一個重要的概念，叫做“固有時”，固體的固，有沒有的有。固有時的意思就是每個觀察者有自己的獨立時間。狹義相對論告訴我們，這個宇宙中不存在一個統一的時間標準，每一個處在不同參考系中的觀察者，都有一個屬於自己的固有時。不同觀察者之間的時間流逝速度差異可以被精確地計算出來。

但我想說，這樣理解狹義相對論，只能停留在高中生水平上。更進階一點的理解是，狹義相對論把時間也看成是跟空間一樣的維度。我們生活的這個宇宙有三個空間維度，就是我們常說的上下、前後、左右這三個互相垂直的方向。實際上，還有一個我們看不見的第四個維度，就是時間。

狹義相對論把時間和空間統一了起來，它們一起構成了我們所生活的四維時空。愛因斯坦石破天驚地指出，時間和空間是一個整體，它們並不是互相獨立存在的。當我們運動起來時，我們眼中看到的一切都會發生變化，不僅是空間，還有時間。時間和空間他們是無法分離的，如果把空間看成是一張漁網上的洞洞，那麼時間就是編織漁網的線。想想看，洞洞和魚線之間是什麼關係，它們不可能獨立存在，改變洞洞的大小必然改變魚線的結構，改變魚線的結構也必然改變洞洞的大小。

我知道，對於普通人來說，不僅難以接受，甚至很難想象時間怎麼能變呢？但愛因斯坦的驚人想法卻經受住了嚴苛的實驗檢驗，被無數的實驗精確地證實，時間確實會因爲運動而改變。

狹義相對論可以用這樣一句話來定義：它描述了時間、空間、運動這三者之間的數學關係。它爲人類貢獻了“時空”這個概念，請務必注意，時空不是簡單的“時間+空間”的意思，就好像“牛奶”不能簡單地理解爲“牛+奶”一樣，時空就是時空，它是一個完整的概念。

有了“時空”的概念後，我就可以來跟你講講“時空彎曲”是怎麼回事了。

彎曲空間的數學定義

要理解時空彎曲，我們先從“彎曲”的概念說起。我在白紙上畫一根曲線和一根直線，你一眼就能看出哪根是直線，哪根是曲線。這是因爲我們都知道這樣一個基本原理：兩點間直線最短。所以，在平面上，我們可以把直線定義爲：過兩點最短的那根線就是直線。

我們再來看一個球面的情況，你想象一下，在一個籃球上，能不能畫出直線。你可能會覺得不能，籃球上的所有線，不管怎麼畫，在我們看來都是曲線。但如果我們考慮一隻在籃球上爬行的螞蟻，在它的眼中，就有直線了。螞蟻會認爲，我從籃球上的一個點爬到另外一個點，路徑最短的那根線就是直線。這個定義和平面上的直線定義是一致的，非常優美，也很合乎邏輯。並且，有意思的是，數學家很容易證明，如果沿着最短路線把籃球一切兩半，切出來的剖面一定是通過球心的，而兩半的大小也恰好完全相等。這條路徑被稱爲測地線。

我們的地球幾乎就是一個標準的球體，在海上航行的船隻，沿着測地線航行，走過的路徑就是最短的。

有了這個鋪墊，我們現在再來想象我們所生活的這個三維空間。

現在，我們需要把自己想象成卑微的螞蟻，我們就好像在籃球上爬行的螞蟻，無法跳出我們所處的這個空間，用更高維的視角來看。那麼，我們該如何定義三維空間中的直線呢？可以沿用平面上的定義，就是把空間中的直線定義爲兩個點之間的最短路徑，這個定義在數學上是一致的，非常優美，物理學家們也完全接受這個定義。

但接下來就面臨一個問題了，我們怎麼才能知道空間中兩點的最短路徑到底是哪條路徑呢？這個問題看似簡單，其實一點也不簡單。你閉上眼睛想象自己漂浮在黑漆漆的宇宙中，前方有一個目標，你從自己所處的位置前往那個目標，會有無數條不同的路徑可以走，就好像螞蟻在籃球上從一個點爬到另外一個點，有無數條路徑一樣。那麼到底哪條路徑纔是最短的呢？

物理學家給出了一個答案，很簡單：我們假設光走過的路徑就是最短路徑。

你看，這裏我又用了“假設”這個詞，但實際上，這個答案也可以被稱爲“費馬原理”。如果你還記得我前面跟你講的光速不變原理，你應該知道，其實不管是假設、原理、約定、信念，它們的含義其實是一樣的。物理學家們都相信，光永遠按照最短路徑在空間中運動，雖然這個信念無法被完全證實，但我們也沒有觀察到任何反例來推翻這個信念。這樣一來，根據直線的定義，空間中的兩點，光走過的路徑就是直線。

好了，有了這個基礎概念。我就可以跟你解釋清楚什麼是時空彎曲了。假設，光從空間中的一個點走到另一個點，路徑發生了變化，我就可以認爲這個空間發生了彎曲，而時間和空間是一個整體，空間發生了彎曲必然會導致時間也跟着彎曲，所以，準確地說，是兩點之間的時空發生了彎曲。

廣義相對論：物質與時空的對話

聽到這裏，你可能還是有點不相信，光走過的路徑難道真的會變嗎？真的會變。當愛因斯坦在 1911 年首次提出這個想法時，絕大多數物理學家都認爲他瘋了，因爲，過去從來沒有哪個天文學家或者物理學家觀察到過光的路徑會發生改變。不過，愛因斯坦不僅提出光的路徑會改變，還精確地計算出，當遙遠恆星發出的光掠過太陽時，從我們地球觀察，會發現星光被彎曲了 1.75 角秒。並且，愛因斯坦還預言，只要在發生日食的時候給太陽周圍的恆星拍照，就能證實我的預言。

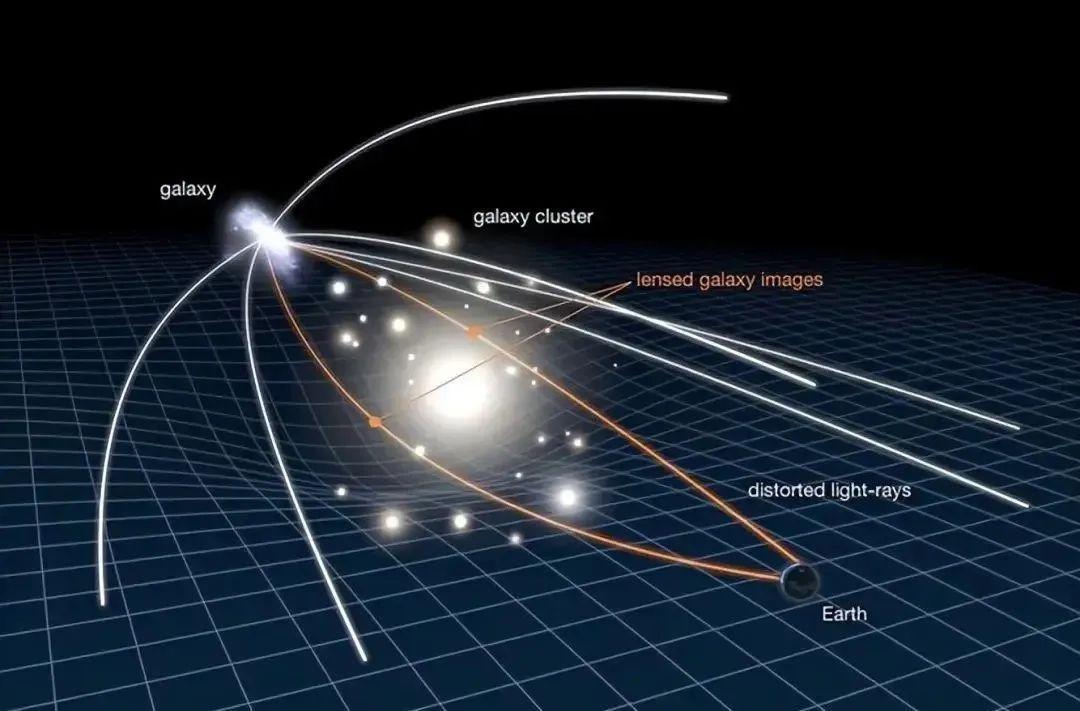
科學理論最重要的特徵就是不僅可以定性，還能定量。定量化程度越高，越精確，也就意味着這個理論越成熟。這也是科學理論和哲學觀念的重要區別。很多哲學家都會提出各種各樣定性的觀點，比如著名的民間哲學家王東嶽就提出了“遞弱代償”的哲學觀念，我且不論這個觀念是否經得起檢驗，我必須指出，這是一種哲學觀念不是科學理論，因爲這種觀念只能定性地解釋一些自然現象，卻無法做出準確的可量化的預言。其實，我也不認爲王東嶽提出的遞弱代償是個正確的哲學觀念，因爲這個觀念的反例也有很多，王東嶽也是一位只在民間有影響力的哲學家，在學術界，並沒有任何影響力。科學理論不僅要能定量，而且是不能有任何反例的，只要出現了反例，就說明這個理論至少是有瑕疵，需要被修正。

1919 年，英國著名的科學家愛丁頓帶領着考察隊成功驗證了愛因斯坦的預言。當然這裏插句題外話，也有一些材料說其實當時愛丁頓爲了能證實愛因斯坦的預言，對拍到的照片做過一些數據修正。不過，後來又有很多科學家都在日食發生的時候成功驗證了愛因斯坦的預言。從此，愛因斯坦的廣義相對論名聲大振。因爲時空彎曲的理論，就是愛因斯坦的廣義相對論提出來的。

好了，我們終於從光速不變原理出發，講到了廣義相對論。要理解黑洞到底是什麼，我們必須對廣義相對論有一個基本的瞭解，因爲黑洞是廣義相對論的預言，就好像那個星光彎折的預言一樣。到底什麼是廣義相對論呢？

一句話來說的話，廣義相對論描述了時空的形狀與時空中質能分佈之間的數學關係。這裏出現了兩個關鍵詞，一個是時空的形狀。我想有了我前面關於時空彎曲的鋪墊，你對時空的形狀可能容易接受一些了。既然時空是可以彎曲的，那就意味着它的形狀是可以發生改變的，雖然我們人類就是身處三維空間的生物，不可能用肉眼看到時空的形狀，就好像螞蟻永遠無法看到籃球的形狀一樣。但是，我們卻可以建立一個數學模型，把看不到的時空形狀給精確描述出來。或者你也可以這麼理解，有了廣義相對論，我們就可以精確地預言兩樣東西：

1. 光在某個空間中會走過怎樣的路徑；

2. 這個空間中每一個點的固有時之間的差異。也就是說，可以精確地預言時空的變化。

那通過什麼東西來預言呢？答案是通過觀察和計算空間中的質能分佈情況。這裏的質能指的就是質量和能量的意思。比如說，太陽、水星、金星、地球、火星這五個天體所在的空間範圍，天文學家們稱之爲內太陽系。在這個空間中，太陽是毫無疑問的質量中心，貢獻了 99.9994% 的質量，但水星、金星、地球和火星的質量雖然佔比很小，也並不是零。另外，如果我們以太陽爲參照物，其他行星都圍繞着太陽公轉。每一顆行星就像是一列高速行駛的火車，含有巨大的動能，這些動能在空間中的分佈隨着時間的變化而變化。這就是我所說的質能分佈。

好了，現在天文學家們如果精確測量出了每一個天體的質量，又測量出了這些行星的繞日軌道週期，利用廣義相對論，就能準確地描述內太陽系的時空形狀了。只要科學家們願意，就可以計算出內太陽系任意兩點間，光會走過怎樣的路徑。也可以計算在內太陽系的任何兩個點之間的時間流逝的速度差異。是不是很厲害？

所以，廣義相對論的方程雖然很複雜，但如果我們從宏觀上理解倒也不難。方程是一個等式，等式的左邊描述了時空的形狀，等式的右邊描述了時空中的質能分佈，或者也可以說是質量、動量的分佈。

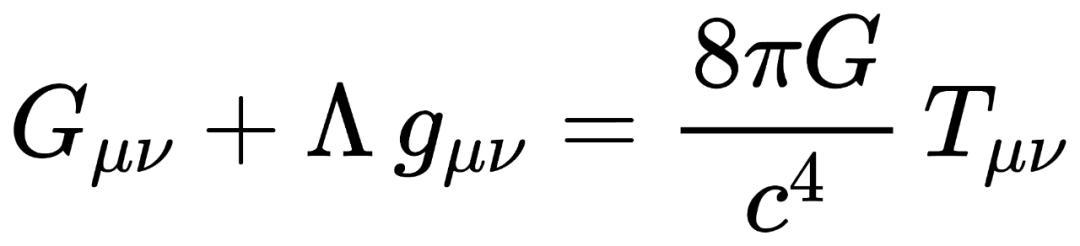
學過小學數學的我們都知道，方程式的左右是可以互換的，A = B 也可以說是 B = A，因此，我們如果準確測量出了某個空間的時空形狀，也能準確地預言在這個時空中的物質會如何運動。

正是因爲這個原因，著名的物理學家惠勒纔會說出他的那句名言：物質告訴時空如何彎曲，時空告訴物質如何運動。

剛纔我提到，廣義相對論的方程，也被稱爲愛因斯坦場方程，從宏觀上理解它的含義並不難。但是，要從數學的角度去理解並計算它，卻是相當相當的困難。

這個方程如果全部展開，是 10 個偏微分方程，而且不是單獨的偏微分方程，是 10 個耦合在一起的方程，無法獨立分塊求解。什麼意思呢，就是說每個方向的彎曲都和其他 9 個方向關聯，牽一髮動全身。

下面讓我用一個比喻來形象說明爲什麼解廣義相對論方程那麼困難，你可以把這個方程想象成一張自己會彎曲、還能把座標紙拉伸撕裂的“橡皮膜”：你得同時決定膜上每一點的形狀，又要保證整張膜不會被拉壞，還得滿足各種邊緣條件，比如如何處理無窮大，無窮小，無窮遠之類的。這就讓它比普通的“先畫座標、再算曲線”的方程難得多。我們中學時學過的那些方程，都是先固定好了座標系，然後在裏面算各種方程對應的曲線，或者曲線對應的方程。但愛因斯坦的場方程，就像是座標系和曲線都會發生互相影響，非常非常麻煩。

如果你覺得我剛纔這個比喻還是有點難理解，那我再給你換個更通俗的比喻。我們做牛頓力學的那些習題，就好像是在把一根繩子上打的結給解開。這個結不論打得多麼複雜結實，它總歸只有兩個頭，我們只要找到其中一個頭，按部就班地一點點解，總是能解開的，最多就是時間長，不會讓我們抓狂對吧。但是，解愛因斯坦的場方程，就好像是給你一個巨大的亂麻團，你也不知道里面有幾個線頭，所以，你去解的時候，經常會以爲解開了一個結，其實是在另一個方向上打了個新結，你想象一下那種令人抓狂的場景。不知道這次有沒有了一點感覺。

你別看這個方程是愛因斯坦自己搞出來的，其實，他自己也不太會解，他也在奮力地去尋找滿足這個方程的一個個解。

這裏我解釋一下，什麼叫“一個個解”。如果你還是小學生，可能不知道一個方程中的未知數有時候會不止一個答案，一個答案就是一個解。學過中學數學後，我們就知道，只有一個解的方程反而是少數，大多數方程都不止一個解。

愛因斯坦的場方程那理論上可以有無數多個解，但要找到任何一個解都不容易。每找到一個解，就意味着我們找到了一個特定形狀的時空區域，在這個區域中，我們既知道它的時空形狀，也知道里面的質能分佈情況。當然，這個時空區域有可能是穩定不變化的，也有可能是隨着時間變化。總之，每多找到場方程的一個解，就意味着我們對宇宙會產生怎樣的特定時空區域多了一分預測。

1915 年12 月 2 日，正是第一次世界大戰硝煙正濃的時候。身爲德國普魯士科學院院士的愛因斯坦住在柏林，他歷經 10 年才正式完成的場方程，這一天正式發表在德國《普魯士科學院會議報告》上。這份報告將被寄往全世界各地的訂閱者。

幾天後，在東線戰場的一個火炮觀測所中，一名炮兵中尉拿到了自己訂閱的《會議報告》，他立即就被深深地吸引住了。此時的他，就像着了魔似的，在極其惡劣的環境以及深受皮膚病困擾的條件下，開始了瘋狂的計算，戰場上震耳欲聾的炮火聲也無法阻止他的筆。

20 天后，這名炮兵中尉把自己的計算手稿寄給了愛因斯坦，裏面有他解出的一個精確解。幾天後，愛因斯坦驚訝地收到了這份還帶着戰場氣息的手稿，他立即被這份手稿中展現出來的高超數學技巧折服，這是一個場方程無比優雅的解，推導過程也簡潔漂亮。1916 年 1 月，在普魯士科學院的會議上，愛因斯坦向所有院士，莊重地宣讀這份手稿。

正是這份手稿，開啓了人類對黑洞的研究。

這名炮兵中尉到底是誰？他又有着怎樣的傳奇故事？科學有故事，我們下期接着聊！

你喜歡本期文章嗎？歡迎在評論區留言。