得過諾獎的數學家

英國數學家羅傑·彭羅斯(Sir Roger Penrose,1931-)
撰文 | 張天蓉
● ● ●
諾貝爾獎在科技界的地位無可非議,遺憾的是它沒有數學獎。不過,也有幾位數學家得到了諾貝爾獎。本篇的主角,英國數學家羅傑·彭羅斯(Sir Roger Penrose,1931-),就與兩個諾獎有關。
之前介紹過的“王浩瓷磚”,屬於“非週期性密鋪”圖案,由11個王氏磚組合成一組,可以實現一種非週期性密鋪。所謂“非週期性”,意味着將密鋪的一部分,不旋轉地移動有限距離,不會產生完全相同的密鋪圖案,也就是說,圖案不具有平移對稱性。通俗地說,就是可以用這一組瓷磚,一直鋪下去但圖案永不重複。這一組瓷磚叫做“原始瓷磚”。
由王氏磚研究的啓發,有人便思考如何用更少數目不同原始瓷磚的組合,來實現非週期性密鋪。結果得到一個較小的數目:2,例如彭羅斯密鋪。
彭羅斯密鋪
沒有周期的密鋪是非週期的。如果一組原始瓷磚構成的所有密鋪都是非週期的,則稱爲非週期密鋪。非週期密鋪比周期性密鋪更具趣味性,在數學研究中也更有意義,比如王浩瓷磚,能與圖靈機聯繫起來。彭羅斯密鋪也很有意思,它是已知最簡單的由有限原始瓷磚構成的平面非週期密鋪的重要例子之一。
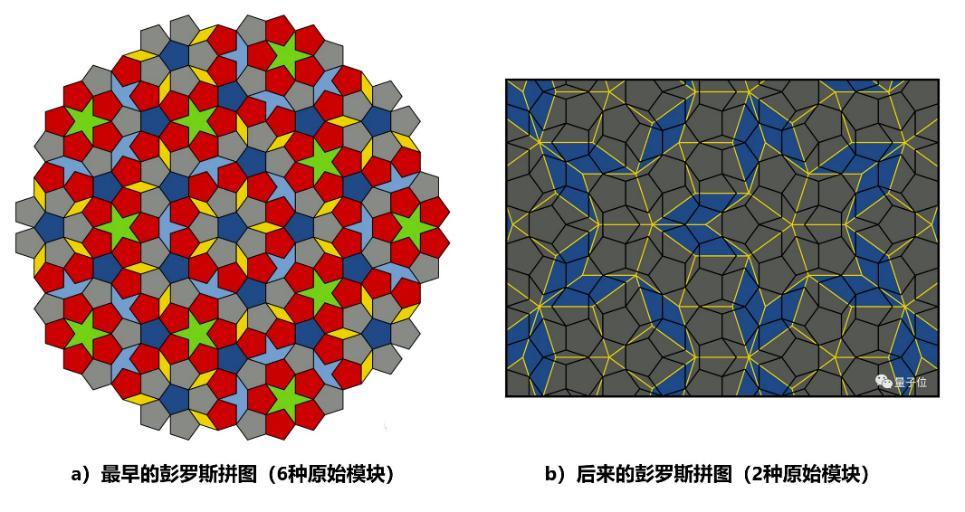
圖1:兩種等效的彭羅斯密鋪(原始瓷磚數不同)
第一個彭羅斯密鋪,由六個原始瓷磚組成,由彭羅斯在1974 年的一篇論文中引入[1],它基於正五邊形而不是正方形。我們知道,任何用正五邊形拼貼平面的嘗試都必然留下空隙,但這些空隙可以用五角星以及其他形狀填補。彭羅斯找到了這些形狀的匹配規則,得到了一個六種原始瓷磚的非週期集,見圖1a。在圖1a中,六種原始瓷磚用六種不同的顏色表示,其中有三種顏色的正五邊形,它們被看作是不同的原始瓷磚,是因爲它們遵循的匹配規則不同[2]。
隨後,彭羅斯將原始瓷磚的數量減少到兩個,發現了菱形密鋪和風箏飛鏢密鋪兩種類型,見圖1b。這個發現由馬丁·加德納在 1977 年 1 月的《科學美國人》 “數學遊戲”專欄中發表。
從圖1中可見,彭羅斯這種密鋪方法拼出來的圖案,沒有周期性,但卻具有五次對稱性。
密鋪與諾貝爾獎
彭羅斯的密鋪是他衆多數學小作品中的一個。不過,這個“小”數學遊戲,卻使另一位以色列科學家舍特曼受益匪淺,獨自獲得了2011年諾貝爾化學獎,以表彰他“對準晶體的發現”。
1982-1984年,材料科學家丹·謝赫特曼(Dan Shechtman,1941-,丹尼爾·舍特曼)(圖2),在電鏡下觀察快速冷卻的鋁錳合金時,發現了一種新的金屬相,其電子衍射斑具有明顯的五次對稱性,這是一種新形態的二十面體相(Icosahedral Phase)分子結構,見圖2右。

圖2:謝赫特曼和銀鋁合金準晶的原子模型
然而一開始,謝赫特曼的新發現沒有被主流化學界認同,別人都不相信他的說法,原始文章也難以發表,使謝赫特曼感到分外沮喪。
權威們爲什麼會反對呢?因爲根據晶體結構理論,晶體就是空間中有周期重複的對稱性排列。週期重複對應於數學中的平移,因此,晶體中的原子格點,需滿足平移對稱性。如此一來,原子格點只可能具有2、3、4、6重的旋轉對稱性,不可能具有謝赫特曼所觀察到的5重旋轉對稱性。換句話說:5重旋轉對稱不能與平移性共存,而平移對稱是晶體的基本特徵。
謝赫特曼相信自己多次實驗所見到的事實,爲了解釋這點,他提出一種解釋,認爲晶體可能有時會出現“非週期性” 的圖案。這種解釋遭到科學界的敵視和嘲諷。萊納斯·鮑林甚至說他在“胡說”,“沒有僞晶體,只有僞科學家。”,上司告訴他,“回去讀教科書”,“讓他停止爲團隊‘帶來恥辱’。”
最後,彭羅斯早就發現了的數學拼圖方法幫助了謝赫特曼,讓晶體研究者們認識到5重旋轉對稱的非週期結構的確是真實存在的,加上後來接連不斷的其他類似實驗結果的發現。人們才認識到這是一種新物態,類似晶體又不完全是晶體,故稱之爲“準晶體“。
比較圖1和圖2,可以看出,彭羅斯密鋪與謝赫特曼發現的銀鋁合金準晶體原子模型的相似性。
兩年後,謝赫特曼的文章得以發表。2011年,他獨享該年的諾貝爾化學獎[3]。
彭羅斯自己的諾獎
9年之後,彭羅斯自己也得了諾獎,不是因爲容易理解的拼圖小遊戲了,而是與“黑洞”有關。他因爲“發現黑洞的形成是對廣義相對論的有力預測”,而榮獲了2020年度的諾貝爾物理學獎。
羅傑·彭羅斯出生於英國埃塞克斯郡,一個顯赫的學術家族。祖父母是愛爾蘭裔藝術家;父母都是精神病學家和遺傳學家;兄弟姐妹皆爲學術精英。彭羅斯的父親在智力障礙遺傳學方面進行了開創性的工作,同時也是著名的數學家和國際象棋理論家,這點對彭羅斯的成長影響巨大。
二戰期間,彭羅斯在加拿大度過了童年,隨後,他進入倫敦大學學院,並於1952 年完成本科,1957 年在劍橋大學獲得代數幾何博士學位。
彭羅斯本科時便開始了他的學術生涯,作出不凡的成績,90歲之後仍然參與學術活動。
彭羅斯得到諾貝爾物理學獎的工作,是他作爲“數學物理學家”的成果。1964 年,彭羅斯研究廣義相對論的彎曲幾何,使用與約翰·惠勒發展的微擾論不同的更具創新性的方法,即忽略時空的詳細幾何結構,而只關注空間的拓撲結構。彭羅斯在1965年發表的劃時代重要論文《引力坍縮與時空奇點》[4]中提出,如果一個物體(例如後期恆星)在某個點之後內爆,那麼沒有什麼可以阻止引力場變得如此強大以形成某種奇點,是他對黑洞引力塌縮理論之最早陳述。
彭羅斯比公衆熟知的霍金年長10歲左右,他曾擔任霍金博士答辯的評委。彭羅斯在廣義相對論工作中的第一條奇性定理,對霍金的研究有所啓發,之後,他們倆又一起證明了廣義相對論中的“彭羅斯-霍金奇點定理”。彭羅斯在引力坍縮的局部背景下做出了最具決定性的貢獻,除了1965的論文之外,他1969 年提出宇宙審查猜想,之後與霍金完成的共同工作,爲黑洞之引力塌縮理論奠定了基礎,無愧於2020年的諾貝爾物理獎。
在宇宙學方面,彭羅斯提出了一個頗具新意的,基於共形映射的循環宇宙的思想,即彭羅斯共形循環宇宙(CCC)的數學模型(圖3),詳情見筆者的另一篇文章[5]。
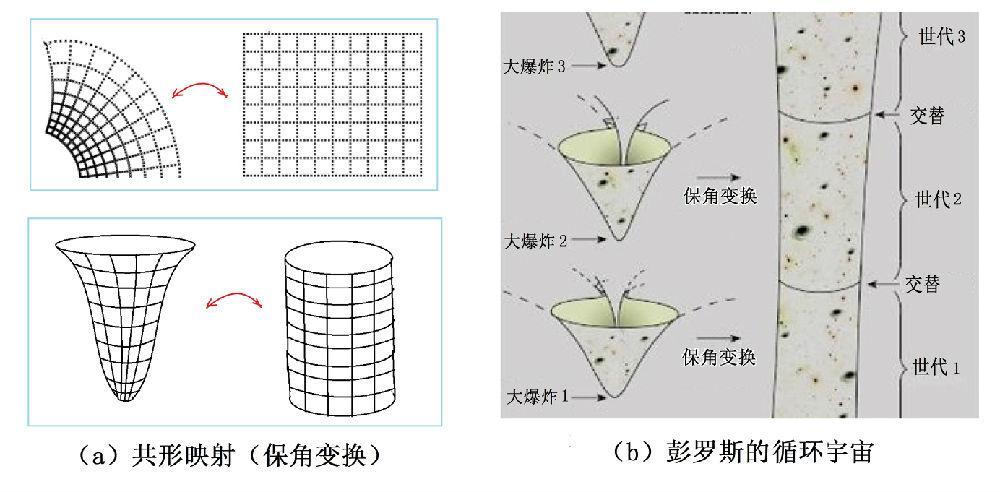
圖3:彭羅斯將共形映射應用於循環宇宙模型
彭羅斯也是一位科學哲學家及思想家,他興趣廣泛,知識淵博,出版過一系列與科學哲學相關的著作,也與霍金及其他同行一起合著過好幾本有關宇宙、大爆炸等的普及讀物。他寫過很多關於基礎物理學和人類(或動物)意識之間聯繫的書籍,其中有一本廣爲人知的科普書,中文版叫《皇帝新腦》,討論量子物理與人類意識的關係等等。彭羅斯是“少數相信意識的本質意味着量子過程的科學家之一”。
雖然彭羅斯得的是諾貝爾物理獎,但他在物理界的確屬於“少數派”,他有許多古怪的、與衆不同的想法,這位如今已94歲的學者,經常用他抽象的數學眼光來“挑剔”物理,看到許多物理主流理論的缺陷和問題。他用數學的直覺,表達他對物理概念的憂慮:他質疑弦論的額外維度,不相信標準時空,懷疑量子引力等等。當然,這些也仍然是物理中懸而未決的幾個問題,但彭羅斯提出的新方法卻是讓許多人覺得更匪夷所思。據說在某一次會議上,物理學家薩斯金對彭羅斯說過一句極具代表性的“真”話:“當然,你可能完全正確的,卻迷失了方向!”意思是,您就算對了,也和我們走的不是一條路啊!
彭羅斯樓梯及其他
也許在學術界,彭羅斯更是一位成功的數學家。他原來的專長是代數幾何學,在幾何方面,有許多完全可以被普通老百姓所理解,又十分有趣的成果及哲學思考。比如彭羅斯地磚,就可以在日常生活中直接應用。
彭羅斯對幾何有一種與衆不同的直覺。他從小對“不可能”的東西感興趣,並且善於從“不可能”中,發現其隱藏於深層的祕密。彭羅斯密鋪瓷磚也是一例:局部看起來圖案是對稱的,也具有整體對稱性,如果一直鋪下去呢?好像“不可能”不重複,應該是週期的吧?但結論卻不是!
在劍橋讀書時的數學會上,彭羅斯看見了埃舍爾的畫,十分感興趣,啓發他與父親合作設計並推廣了“彭羅斯三角形”,後來演化成“不可能樓梯”(圖4)。之後,父子倆與埃舍爾有了很多互動,彼此交換素材,互相啓發思維。彭羅斯從數學的角度研究不可能圖形的上同調,埃舍爾以畫家的觀察,產生了《瀑布》、《升與降》等膾炙人口的作品。
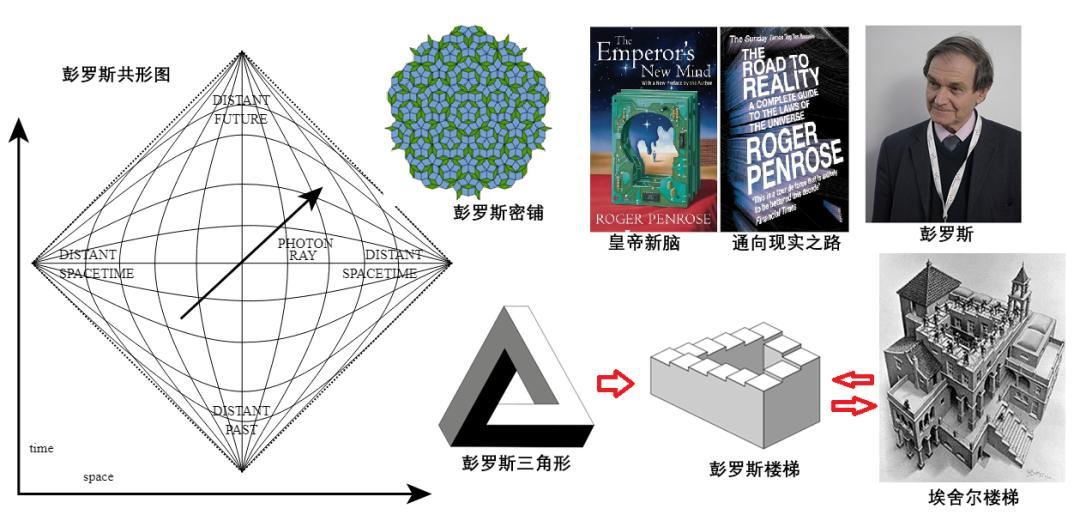
圖4:彭羅斯用直觀的幾何表達哲學思想
這些“不可能”的幾何思考,必然對彭羅斯的學術研究有所影響。1967年,彭羅斯發明了扭子理論,將閔可夫斯基空間中的幾何對象映射到四維復空間中,他認爲全純的扭量應該是時空的最基本結構。雖然他的扭量理論在數學圈有一定影響,但物理響應不多。
彭羅斯在1971 年發明自旋網絡,後來形成了圈量子引力中的時空幾何,再看看他的的彭羅斯共形圖(圖4左圖),他將無限的時空,用一個有限的圖形表示出來,將無限映射到有限,這實際上就是一種“不可能”幾何的具體實現。還有彭羅斯“共形循環宇宙學”,其淵源是有趣的外爾曲率。從這些有關時空結構的研究中,都能看到彭羅斯幾何表象下的哲學思考。
彭羅斯的成果如此之多,我們可以來一趟“彭羅斯世界之旅”:踏上彭羅斯密鋪地,走下彭羅斯階梯,手舉彭羅斯三角形,眼觀彭羅斯共形圖,思考彭羅斯無限循環的共形宇宙,考察其中的奇點效應……
當然,要真正瞭解這位多產的科學家,是讀他的書。彭羅斯的幾本書,都有中文版,如《皇帝新腦》和《通向現實之路:宇宙法則完整指南》。其中許多有趣的想法,也包括彭羅斯
對他自己理論的解釋等,值得一讀。
參考文獻:
(上下滑動可瀏覽)
【1】Penrose, Roger (1974). "The role of aesthetics in pure and applied mathematical research". Bulletin of the Institute of Mathematics and Its Applications. 10: 266ff..
【2】Original pentagonal Penrose tiling (P1):https://en.wikipedia.org/wiki/Penrose_tiling#CITEREFPenrose1974
【3】維基百科:丹·謝赫特曼,https://zh.wikipedia.org/wiki/%E4%B8%B9%C2%B7%E8%B0%A2%E8%B5%AB%E7%89%B9%E6%9B%BC
【4】Roger Penrose,Gravitational Collapse and Space-Time Singularities
,Article in Physical Review Letters, published January 1965,DOI 10.1103/physrevlett.14.57,pub.1060767972
【5】科學網-博文,https://wap.sciencenet.cn/home.php?mod=space&uid=677221&do=blog&id=979548