你或許也有過這樣的經歷：搬家時，想在狹窄的空間裏移動傢俱，結果在轉彎時被卡住，怎麼轉都轉不過去。數學家將這一難題稱爲“移動沙發問題”。

2024年12月2日，韓國數學家白真允（Jineon Baek）在社交媒體上宣稱自己已解決這一問題，隨即在國內外媒體和數學界引發廣泛討論。也許你會好奇：看似一個與日常生活緊密相關的小問題，到底有多難？

移動沙發問題涉及形狀如何適應拐角的數學問題 （圖片來源：加州大學戴維斯分校）

“移動沙發問題”是什麼？

事實上，“移動沙發問題”是一個經歷了許多討論與探索的問題。早在20世紀60年代，一些數學家就已經開始探討與這一問題相關的幾何優化問題。

1966年，奧地利裔加拿大數學家李奧·莫澤（Leo Moser）在正式的數學刊物中首次提出了“移動沙發問題”的明確數學定義和問題描述：在寬度爲1的L形平面走廊中，能夠通過一個直角轉彎而不發生碰撞的“沙發”的最大面積是多少？這一問題自此引起了數學界的廣泛關注，併成爲經典的幾何優化問題之一。

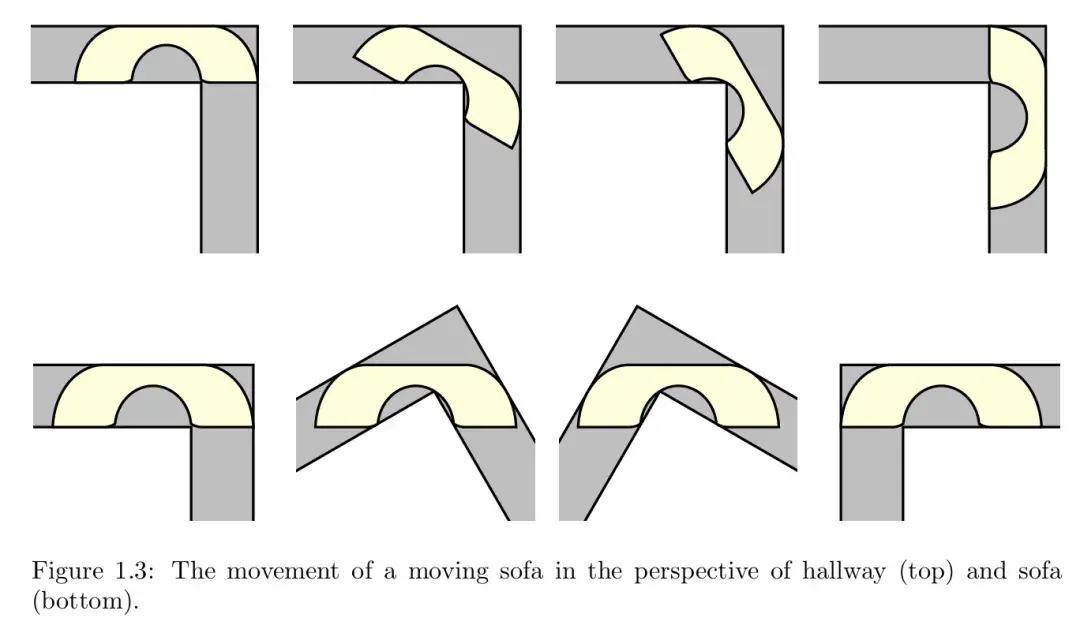
移動沙發問題演示 （圖片來源：文獻[1]）

1968年，英國數學家約翰·邁克爾·哈默斯利（John Michael Hammersley）根據最簡單的情形提出了一種解法。他將“沙發”設計成類似於一個電話聽筒的形狀，由兩個四分之一圓和一箇中間的矩形塊組成，中間的矩形塊中挖去了一個半圓形，從而得出的“沙發”最大面積爲。

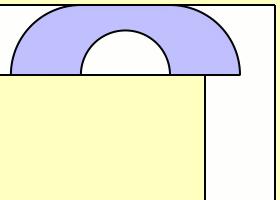
哈默斯利設計的“沙發” （圖片來源：維基百科）

1992年，美國數學家約瑟夫·傑弗（Joseph Gerver）在哈默斯利設計的“沙發”的基礎上進行了改進，提出了一種由18條光滑曲線圍成的“沙發”，算出的最大沙發面積約爲2.2195，進一步提高了這個問題解的下限。

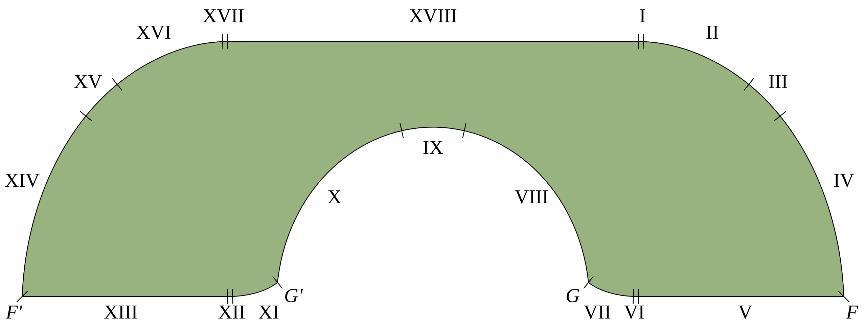
傑弗設計的“沙發” （圖片來源：維基百科）

又到了2014年，業餘數學家菲利普·吉布斯（Philip Gibbs）通過計算機演算得出了一種最優沙發形狀，其與約瑟夫·傑弗（Joseph Gerver）設計的“Gerver沙發”幾乎相同，且計算出的面積在八位有效數字下相同。這一發現表明，傑弗設計的“沙發”很可能就是移動沙發問題的最優解，不過這一點尚未得到數學上的正式證明。

不過，科學家們至少已經確定了“沙發”面積的一個上限，也就是這個面積最大不能超過多少。哈默斯利指出了沙發常數的上限最多爲。2018年，約阿夫·卡魯斯（Yoav Kallus）和丹·羅米奇（Dan Romik）通過將走廊（而不是沙發）旋轉幾個不同角度，使旋轉後的走廊交集形成儘可能大的連接區域，並利用計算機搜索，成功將“沙發”的上限縮小至2.37。

也就是說，“移動沙發問題”的最優解在2.2195～2.37之間。

“移動沙發問題”到底難在哪？

看到這裏，你可能會問：“移動沙發問題”看起來如此直觀簡單，爲什麼卻困擾數學家超過半個世紀？

儘管約瑟夫·傑弗已經提出了一個近似最優解，但要證明它就是真正的最優解仍然非常困難，因爲這需要排除所有可能存在的更優形狀。而在平面內，“沙發”的形狀可以千變萬化，最優解很可能是一個不對稱、複雜且不規則的多邊形。

要探索所有可能的形狀並評估其面積和可移動性，涉及極爲龐大的計算量，這使得窮舉所有可能性成爲不可能。此外，既缺乏對稱性和規則性，又能靈活轉動和移動的形狀在幾何上本身就非常複雜，因此，數學家們也難以找到一個通用的公式來解決這一問題。

進入新世紀後，隨着計算機技術的飛速發展，數學家們開始廣泛採用計算機輔助設計和運動路徑模擬，探索“沙發”可能的形狀。然而，即使是使用計算機輔助的數值方法和優化算法，現有的算法在排除所有潛在的更優形狀，以及探索和驗證各種複雜形狀的可行性和麪積時，依然常常面臨計算時間過長和計算資源消耗過大的問題，這在很大程度上限制了進一步研究的進展。

而近年來很火的機器學習在解決“移動沙發問題”時也受到很大限制。機器學習模型通常需要大量的數據進行訓練，而“移動沙發問題”的解答主要依賴於理論推導和優化算法生成的有限數據集，難以滿足大規模模型的訓練需求。

此外，數學優化問題往往需要高度可解釋和精確的解決方案，而機器學習模型的“黑箱”特性使其可能只能給出答案，給不出解決過程，這使得其難以直接應用於此類問題的求解。

“沙發”不僅需要通過直角轉彎，還必須避免與走廊的牆壁發生碰撞，這些多重約束條件使得優化過程極爲複雜。“移動沙發問題”涉及幾何學、優化理論和計算幾何等多個學科的知識，因此需要跨學科的研究來尋找解決方案。

“移動沙發問題”真的被解決了嗎？

讓我們將目光轉向近期備受關注的白真允（Jineon Baek）那篇長達119頁的論文。他宣稱，自己已證明由約瑟夫·傑弗設計的那款“沙發”就是最優解。

白真允首先提出了最優“沙發”的形狀限制條件：①沙發的形狀可通過旋轉走廊的交集定義；②沙發的邊長需滿足特定的平衡條件；③必須能夠旋轉90度完成移動。

接着，他證明了“沙發”在運動過程中，其關鍵點的軌跡不自交（即沒有重複或重疊），形成平面上的簡單閉曲線，從而確保了面積計算的嚴謹性。

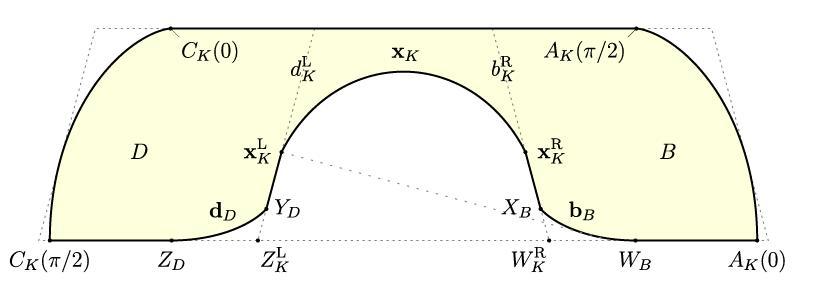
Q(S)定義的圖示 （圖片來源：文獻[1]）

隨後，他構造了一個二次函數Q(S)作爲“沙發”面積的上界，並利用Mamikon定理和Brunn-Minkowski理論證明了Q(S)是凹函數，這意味着它的局部最大值也是全局最大值。

最後，他驗證了傑弗設計的“沙發”完全符合這些條件，且Q(S)的值在此達到最大，確認其面積2.2195是理論上的最大值。

不過，這篇論文尚未見諸權威期刊，也未經過廣泛的同行評審，目前學界對其證明的正確性和嚴謹性仍持觀望態度。要斷言“移動沙發問題”已經徹底解決，恐怕還爲時尚早。

結語

那麼，徹底解決這個問題究竟有什麼意義呢？

除了在解決過程中開發的工具和構造方法爲其他幾何優化問題提供了新的思路外，“移動沙發問題”還可以被抽象爲一種空間利用的極限優化模型，對建築設計、傢俱製造以及物流管理等實際領域具有重要參考價值。例如，在狹窄空間中搬運物體時快遞機器人的路徑規劃，生產流水線上的機械臂搬運不規則物體時的空間路徑規劃，就可以從這一問題的研究中獲得啓發。

讓我們靜待數學家們對白真允論文的審慎驗證，共同期待這一困擾科學界60多年的難題最終得以圓滿解決。

參考文獻：

[1] Baek J. Optimality of Gerver''s Sofa[J]. arXiv preprint arXiv:2411.19826, 2024.

[2] Gibbs P. A computational study of sofas and cars[J]. Computer Science, 2014, 2: 1-5.

出品：科普中國

作者：Denovo

監製：中國科普博覽