硬核 | 信源的「可信度」竟然是可以測量的
本期作者:王木頭 汪詰
上期節目我說:判斷「阿波羅計劃」是否造假,可以用「信源等級」的科學思維去考慮,幫助我們做出選擇。簡單來說,就是我們把發表正反雙方觀點的信源都列出來,然後綜合對比一下這些信源的可靠度的等級,大概率來說,信源等級越高的觀點,越值得我們信任。

今天我想把這個話題展開來談一談。我先提醒一下,本期內容會從一些淺顯的道理開始越講越深,越講越燒腦,以至於到了最後可能 80% 的人無法看到最後。但如果你能認真看到最後,一定會獲得一種窺探到一點點自然真相的滿足感。
▼▼▼
首先,我們快速回顧一下關於信源可靠性等級的排序,按照從高到低往下排是:
1. 國際組織的書面材料
2. 國家級機構的書面材料
3. 入選自然指數科學期刊上的論文
4. 入選 SCI 的核心期刊上的論文
5. 口碑良好的科普類媒體
6. 綜合性大媒體
7. 相關領域知名專家的觀點
8. 相關領域普通專業人士的觀點
9. 非相關專業的實名普通人觀點
10. 匿名網友的觀點
好了,前置知識講完。我們再來看一下關於「阿波羅登月計劃」的爭議。先來找一下認爲阿波羅登月計劃「造假」的觀點都來自哪裏,後面我就簡稱爲【反方】觀點。
我在網上搜索了一下,能找到的信源等級最高的反方觀點是 9 級,也就是來自於非相關專業的實名普通人觀點。
有些人可能會說,馬斯克質疑登月。但馬斯克依然是 9 級,因爲他並不是專業人士,他是太空探索公司的投資人,並不代表就是專業人士。這裏的專業人士指的是:有能力分辨各種證據真僞的航空航天相關領域的科學家或者工程師。還有人可能會提到俄羅斯前航天局的局長羅戈津也在 2023 年 5 月公開說美國人登月造假。羅戈津還是 9 級信源,因爲看一下他的履歷就知道了,他是一個標準的政客。
下面我們來看【正方】觀點的信源。
先說結論,正方觀點能找到的等級最高的信源是 5 級,也就是口碑良好的科普類媒體。我來舉幾個例子,比如:
「科普中國」公衆號,藍 v 認證主體是中國科學技術協會,認證類型是政府。這個可以算是科普媒體的國家隊了,說通俗點兒就是中科協的親兒子。2023 年 12 月 19 日,科普中國發表文章《阿波羅載人登月到底是不是騙局?》,結論很明確,不是騙局。
再比如,同樣是中科協主辦,認證類型是政府的「科學闢謠」公衆號,由中國科協、衛生健康委、應急管理部和市場監管總局等部委主辦,中央網信辦指導,全國學會、權威媒體、社會機構和科技工作者共同打造。
2024 年 5 月 14 日,科學闢謠公衆號發表闢謠阿波羅登月騙局的文章,作者是中國科技新聞學會太空文化傳播青少年工作委員會委員王君毅,審覈專家是中國科學院國家空間科學中心研究員周炳紅。
再比如,我非常推薦的一個科普媒體叫「騰訊較真」,由騰訊公司主辦,也是專門查證謠言的一個科普媒體。2021 年 4 月 15 日發表闢謠阿波羅登月是騙局的文章,作者是行星科學家、中國科學院國家天文臺研究員鄭永春。
另外,像果殼網、知識分子、饒毅科學、風雲之聲、科學聲音等等很多口碑良好的科普自媒體也都發表過正方觀點的文章。
以上例子只舉了中國的,全世界知名的科普媒體發表正方觀點的文章這 30 多年來更是不計其數,搜索結果似乎永遠翻不到頭。
6 級信源是綜合性大媒體,這個要舉例就更多了。比如中央電視臺,出過一個叫「走進真相」的專欄,其中有兩集就是《登月疑雲》,這個節目的播出時間是 2014 年,解釋了很多常見的質疑美國載人登月真假的說法。
另外,像人民日報、澎湃新聞等等很多很多綜合性大媒體都刊登過正方觀點的文章,你很容易檢索到。
7 級信源是相關領域知名專家的觀點,這個也很多很多,比如有着「嫦娥之父」美譽的歐陽自遠院士,他可以說是我國探月工程中最知名的科學家了,他親自錄短視頻闢謠美國登月騙局。其他發表過正方觀點的航空航天專家更是舉不勝舉。
8 級信源是相關領域普通專業人士的觀點,在我們科學聲音專家團中有很多航空航天領域的科學家,他們全部支持正方觀點,無一例外。
好了,講到這裏我總結一下,關於美國載人登月是真是假的正反方觀點的信源等級是 5 級對 9 級,這個落差是非常大的。所以,在面對一些專業問題時,我們可以通過信源等級的比較,來判斷選擇哪方觀點正確的可能性更大。這是一條比較通用的科學思維,對於任何專業性比較強的問題,這條科學思維都適用。
我再強調一下,科學思維不能百分百保證我們每次都能選擇正確,但它是讓我們最有可能找到真相的一種思維方式。
說到這裏,可能有人會好奇,爲什麼正方觀點沒有 1 - 4 級的更可靠信源呢?其實這個也不難理解。
因爲質疑者的身份或問題還不足以讓 1-4 級信源來發聲。
所以,我的觀點是:對於美國登月是不是騙局這件事情,有可能找到的最高等級信源就是 5 級,不可能更高了。
講到這裏,其實我們今天這期節目纔剛剛開始。關於信源可靠度的話題,還遠沒有結束,它背後竟然還蘊含着非常高深的數學原理,讓我們繼續往下深入。
▼▼▼
正如你們看到的,我把信源分成了若干個等級,然後宣稱,等級越高的信源,它的可信度也就越高。
那麼,較真的人可能會追問:這個所謂的「可信度」是可以被測量的概念嗎?如果它根本就不是一個可測量的指標,那你憑什麼說這個信源的可信度要比另外一個信源的可信度高呢?憑你自己的直覺,拍腦袋拍出來的嗎?
這其實是一個非常好的問題,它也是一條科學思維,叫做“沒有測量,就沒有科學”,當我們要給一樣東西定量的時候,必須要說明它的測量方法是什麼,並且是可以操作和計算的。
那麼信源「可信度」這個指標,能不能測量呢?
答案是:能。
那怎麼測量呢?
我先從一個比較容易理解的例子給你講起。
現在,我給你一顆六個面的骰子(色子),請問,你能不能測量這個骰子的可信度?也就是說,判斷出這是一個公平的骰子,還是一顆作弊用的骰子。
我估計,你稍稍一思索就想到了辦法。這個好辦啊,我們來扔骰子,看是不是扔的次數越多,每個面出現的概率越是均等,也就是六分之一,扔上個 100 次、1000 次、10000次,我扔的次數越多,越能證明這個骰子的可信度越高,這個道理不難理解吧。換句話說,一個骰子的可信度,可以通過測量若干次扔骰子的結果計算出來。
我們之所以認爲這個測量方法是靠譜的,背後其實也有一個數學定律在支撐,這個數學定律叫做「大數定律」,意思是:隨着隨機事件的重複次數不斷增加,其平均值將越來越接近總體平均值。這個定律可以用一個嚴格的數學公式來表達:
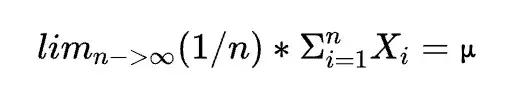
接下來,我們可以把這個測量骰子可信度的方法遷移到測量信源可信度上來,具體怎麼做呢?比如說,我們從每一個信源中隨機選取 1000 篇文章出來,然後給每一篇文章標記上是否被證僞的標籤,被證僞了就得 0 分,沒有被證僞就得 1 分,這樣我們就得到了在同一個測量標準下,每個信源可信度的得分了。我們會發現,不同信源,可信度得分果然是不一樣的,而且,隨着我們採樣的文章越來越多,每個信源得分佔總分的比值也會越來越趨於穩定。
不過,這個測量方法實在太過於理想化了,聽上去好像很有道理,其實你真要去操作,就會發現,這個方法幾乎不可行。因爲,很難給一篇文章用 0 或者 1 去標記,這個世界是複雜的,一篇文章往往幾千、幾萬個字,怎麼評價它是 0 還是 1 呢?如果一篇文章有 60% 的內容是對的,40% 的內容是錯的,那你是標 0 還是標 1 呢?
所以,真實世界要比理想化的模型複雜太多了?那怎麼辦呢?辦法當然是有的,要理解這個升級版的信源可信度測量方法,我們首先要理解一個重要的統計學概念,這個概念叫「似然」,這是一個非常高能的概念,你需要打起精神聽我講解。
▼▼▼
什麼是「似然」呢?我現在用拋硬幣來舉例說明。
假如說,有一個硬幣被動過手腳了,它不再是公平的,而是出現正面的概率要多於反面的概率,它正面朝上的概率是 0.6。那麼請問,如果拋 10 次硬幣,會得到幾次正面幾次反面呢?
這個問題很好回答,大概率會得到得到 6 次正面和 4 次反面。當然,我不是說一定會得到這個結果,而是說大概率會得到這個結果,假如你拋個 100 組,每一組都是拋 10 次,那麼我敢說,這 100 組中,符合正面朝上 6 次的情況是最多的。
剛纔這個問題,就是用已知概率,去推測可觀察結果。是一道最基礎的概率題。
但是,現在我把這個問題的難度提升一下。
假設,你拿到了另外一枚硬幣,你只知道這枚硬幣也是被動了手腳了,只是不知道它具體被動了怎樣的手腳。我要你根據扔硬幣的結果去反推這枚硬幣的正面固有概率是多少,你該怎麼推算呢?
這道題目的難度上升了可不只是一點點,可以說,它非常難。
我來解釋一下。我們現在設想一下,你拿到這枚硬幣,先扔了 10 次,發現,有 6 次正面,4 次反面。這時候,你能不能就宣稱,這枚硬幣的固有概率就是正面 0.6 呢?
顯然不能吧?因爲你才拋了 10 次,次數這麼少。這枚硬幣的固有概率假如不是 0.6 而是 0.4,你拋 10 次,也完全可能出現 6 正 4 反的結果啊。
你可能會想,那 10 次不夠,我們就拋 100次、1000 次,統計出來的結果就是硬幣的固有概率了吧?
也不是。爲什麼?
我舉個例子,假如,你拋了 1000 次,得到了580 次正面,你能宣稱這枚硬幣的固有概率是 0.58 嗎?顯然也不能啊,因爲這枚硬幣的固有概率完全有可能是 0.59 或者 0.57 啊,你拋 1000 次也不可能得到準確的固有概率。並且,這麼往下想是沒底的,即便你拋了一億次硬幣,正面朝上的概率是 0.6,你也不能排除它的固有概率是 0.599 或者其他很接近 0.6 的數。
儘管如此,有一點我們卻是可以肯定的,那就是假如拋出來的統計結果,正面朝上的概率剛好是 0.6,那麼,拋的次數越多,我們就知道,真實的固有概率越接近 0.6,而不會越遠離 0.6。
換句話說,我們拋的次數越多,就會得到一個越接近硬幣固有概率的數值,那麼,怎麼衡量拋的次數和我們得到的這個結果與固有概率的接近程度呢?說得更通俗一點,就是,怎麼衡量我們統計出來的這個數值它就是硬幣固有概率的可信度呢?
在統計學中,就可以把「似然值」當做是衡量硬幣固有概率可信度的度量方式之一。當然,我這裏必須強調一下,這並不是唯一的度量方式,是其中的一種度量方式。
希望你看到這裏已經弄明白了這件事:概率值本質上描述的是一個事件最有可能出現多少次,而似然值則是在描述一個概率值的可信度。
那麼,似然值怎麼計算呢?針對硬幣這個問題,似然值的計算公式如下:
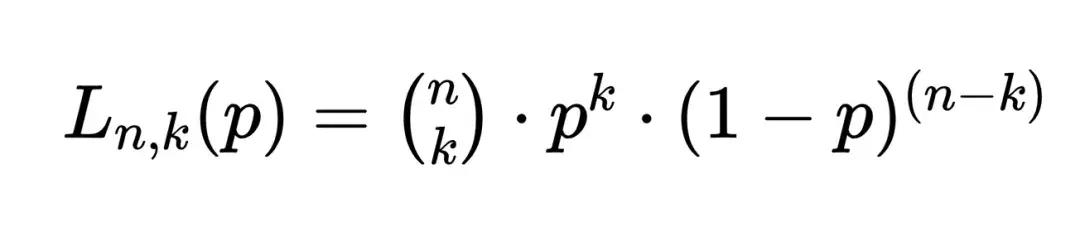
這個公式有三個變量,分別是拋硬幣的次數、得到正面的次數和我們假設的固有概率值,通過一番冪運算,得出似然值。
其實這個似然值,就是先假設一個固有概率,然後去看一下在這個假設之下,發生當前事件的概率大小。概率越高,那就表示可信度越高,反之可信度越低。
我還是來舉例子吧,舉例子最好理解。
假如,你現在拿到一枚硬幣,你扔了 10 次,得到 6 次正面。
那麼,結論是這樣:
這枚硬幣正面固有概率是 0.6 的似然值是 0.2508。換句話說就是,我們完全可以認爲這枚硬幣正面固有概率是 0.6 的可信度是 25.08%。
其實這裏的0.2508,也就是不管固有概率本來是多少,你都假設它就是 0.6,然後去計算一下在這個假設下,拋硬幣 10 次 6 正 4 反的概率值,這個值就是似然值。
上面計算的是 0.6 的情況。那正面固有概率是 0.3 的似然值可以計算出來是 0.0368,也就可以認爲它的可信度是 3.68%。
而正面固有概率是 0.1 的似然值是 0.0001,也就是可信度度迅速下降到了萬分之一。
儘管這個似然值看上去很像是一個概率值,但從準確的數學定義上來說,似然值並不是一種嚴格的概率值。因爲,概率必須滿足歸一性。也就是說,事件發生的概率之和必須是 1。骰子的六個面,每個面出現的概率加起來必然爲 1。但是,似然值並不符合歸一性。就拿剛纔的例子來說,拋出了 6 正 4 反的情況,從正面固有概率是 0.1 到 0.5,再到 0.999,把所有有可能情況的似然值加在一起,它的結果並不等於 1。這裏面涉及的數學問題是題外話,今天不展開說,數學非常深奧。
你看,測量一件事情的“可信度”,它的學問可大了吧。
好了,有了似然值的基本概念,我們又可以回過頭去研究一個信源的“可信度”該怎麼測量的問題了。清醒一下,我們繼續,更燒腦的還在後面。
▼▼▼
儘管,通過拋硬幣統計的方法,拋的次數再多,也不能百分百確定硬幣的真實固有概率,但是硬幣的固有概率的似然值卻是可以定量計算出來的,而且用數學可以證明,在某次測量中,一定會有一個最大的似然值。像是拋出了 6 正 4 反的結果,那麼硬幣正面概率等於 0.6 這種情況的似然值就是最高的,這可以理解爲“可信度”就是最高的。所以,即便是任何一種情況都無法排除,但在必須做出選擇的時候,我們應該理性地選擇 0.6,儘管我們明知,可信度只有約 25%,但它就是在已知條件下可以做出的最佳判斷,是風險最小的選擇。如果選擇其他答案,可信度只會更低,不會更高。
注意,這裏的重點是在已知條件下的最佳判斷,如果我們繼續拋,拋到100次時,結果變成了 30 正,70 反,那麼在有了更多信息的情況下,似然值也會更新,在這種情況下,硬幣的固有概率是 0.3 的似然值就最大了,即可信度最高。
建立了似然值所代表的可信度的基礎概念後,現在我們再看回信源的可靠性這個問題,我們就可以用似然值來計算某個信源的可信度。
之前我們說了,不能只根據一篇文章準確與否就得出信源的可信與否,這樣是非常容易出現偏差的。並且,即便是某一篇文章也不能只用簡單的 0 和 1 來標記,一篇文章本身也有準確度的概念。正確的做法是這樣,舉例來說,假設我們統計了信源發佈的歷史文章,發現 90% 準確的有 21 篇,80%準 確的有 53 篇,70% 準確的有 3 篇,50% 準確的有 12 篇等等等等,然後就我們可以計算,假定該信源是完全可靠的情況下,發佈出這些文章的概率是多少,而這個值,這就是在當前已知的信息下,該信源完全可靠的似然值。換句話說,這個值就可以代表該信源的可信度。
我再解釋一下。某個信源發佈了一篇文章,雖然我們無法百分百確定這篇文章到底是可信的還是不可信的,但是我們可以用“信源完全可靠”和“信源完全不可靠”這兩種假定,來分別計算出它們的似然值。也就是說,先假定信源是完全可靠的,那麼它發佈出這樣的一篇文章的概率值是多少,這個概率值就是信源完全可靠的似然值。
當然,如果你願意的話,也可以假設信源是完全不可靠的,就可以計算它發佈出這樣一篇文章的概率值是多少,這個概率值就是信源完全不可靠的似然值。
不過,在實際生活中,我們只需要用到兩個似然值中的一個就夠用了,沒必要兩個都計算。
好了,講到這裏,我就可以非常有底氣地回答網友的詰問:
信源的可信度能測量嗎?
答案是:能。
怎麼測量?
就是用似然值爲信源的可信度打分,似然值越高,可信度也就越高。
再次強調一點,可信度是 0 到 1 之間的一個概率數字,任何時候,都不代表真理,它只是代表着在當前已知信息的前提下,是我們人類可以得到的最靠譜的結論。
看到這裏,愛較真的聽衆,可能又會拋出另外一個問題:你這種計算似然值的方法,歸根到底還是依賴某人給一篇文章標記百分之多少準確,那假如這個標記本身就是不準確的,這個可信度也就沒有任何意義了。這話當然沒毛病,不過這其實是另外一個話題,我們又要新開一個專題才能講清楚如何避免人爲誤判,簡單來說,這個問題依然可以通過大規模的雙盲評測來解決,這同樣也是個統計概率問題。問題是好問題,但並不是致命問題,聰明的人類早就找到了解決方案。
好,現在我們瞭解了「似然值」這個概念對評估信源的作用了,但我們還要再往下深入一步,看看它在訓練 AI 中所起到的巨大的作用。
▼▼▼
「似然值」在人工智能的訓練工程中又起到了什麼作用呢?之所以會有似然值,本質上是我們把客觀世界裏的各種屬性特徵分成了兩類,一類是可以直接觀測到的屬性,比如前面提到的硬幣落地後的朝向,一篇文章的準確程度,還可以是圖片裏的內容到底是貓是狗等等;另一類是沒有辦法直接觀測到的屬性,比如硬幣的固有概率值,信源的可信度,還有就是人工智能模型裏的參數值等等。在人工智能領域,這部分不可直接觀測得到結果的屬性,往往也被稱作是「隱變量」,一個「隱變量」的所有可能性組成了一個空間,叫做「潛空間」。
而且,往往從邏輯上看,隱變量的取值決定着可觀測變量的取值,所以我們纔可以從可觀測變量反向去窺探一下隱變量的真實數值。只不過,這件事永遠做不到完美,我們只能通過當前有限的數據去儘可能的接近隱變量的真實數值。這個時候就需要似然值了。通過似然值,理論上我們總是可以找到可能性最大的隱變量的取值。對於人工智能模型,你用 100 張狗的照片去訓練模型,那麼只需要找到使似然值最大的那些模型參數,就可以讓模型去判斷這 100 張圖片都是狗的可能性最大。
上面這段話聽着有點繞口,你仔細聽兩遍,一定能理解的。
現在的人工智能模型也的確是這樣做的,總是去追求似然值最大,更專業的說法叫做「最大似然估計」。不論是是現在最流行的多層感知機模型,還是深度網絡流行之前的支持向量機模型,還是上一期介紹過可能挑戰多層感知機地位的 KAN 網絡,它們背後都以一個隱藏目標,就是訓練出一組模型參數,能夠讓似然值儘可能的大。
人工智能追根溯源的話,有兩個最大的分支,最最早期的人工智能模型都是基於邏輯推理實現的,可惜現實裏的邏輯規則過於繁複,幾乎無法窮盡,所以這個分支現在處於破產狀態。另一個分支是基於統計學習的分支,在人工智能發展史上凡是接近實用的模型都是在這一分支下發展出來的,而這一切的基礎,就是去尋找最大似然值。
當然了,人工智能的訓練也不是隻有尋找最大似然值這一個目標,如果只是去實現這一個目標的話,那麼往往就會出現過擬合的情況。也就是說,在已有的數據下,模型的各種表現都很好,一旦超出已有數據,模型的表現力就大幅減少。
一個經典的例子就是,曾經有一個圖像識別模型被訓練來區分坦克和飛機的圖片。模型在訓練集上表現得非常完美,能夠 100% 準確地識別出坦克,然而,當模型被用於新的、未見過的圖像時,它的性能卻非常差。經過進一步的調查,研究人員發現模型並沒有學習到坦克的特徵,而是學習到了訓練圖像中的背景——藍天。因爲在訓練集中,所有的坦克圖片背景都是藍天,而飛機圖片的背景則不同。模型實際上是通過識別圖像中是否爲藍天來做出判斷的,而不是坦克本身的特徵。
所以,一個成功的 AI 模型一定是在追求最大似然值的同時,還會盡力做到,讓模型的泛化能力更強,是對兩個目標綜合考慮後的權衡取捨。其中一個方法,就是將最大似然估計,修正爲最大後驗估計。
完了,看到這裏又出來一個新名詞「最大後驗估計」,但我們今天的內容已經太長了,這個概念就權當是一個懸念留着吧,以後有機會再介紹……