近段時間以來，“社交牛X症”（以下簡稱“社牛”）刷遍全網。所謂“社牛”，指的是可以不在乎他人的想法與目光，徹底放飛自我的社交方式。與“社交恐懼症”相對，是一種無所畏懼的社交方法。

在網絡上，很多患者已經以自己的實際行動詮釋了“社牛”的具體症狀。而作爲多年的“社恐達人”，筆者決定從數學的角度，對“社牛”進行深入的另類解析，同時爲下次與陌生人交流積累談話素材。

社交牛X症的白雪公主 VS 社交恐懼症的喬巴

（圖片來源：giphy.com）

社交的本質：彼此連接的網絡

無論是““社牛””抑或“社恐”，其前提都落腳在“社交”之上，因此有必要在研究伊始給出社交的恰當定義。我們將社會中的人抽象成一個個節點，如果兩個人相互認識，則將對應的兩個點用線段連接，最終我們將得到一個圖，這也是圖論要研究的對象。

（圖片來源：騰訊視頻）

圖 (Graph)是由若干給定的頂點，以及連接兩頂點的邊所構成的圖形，通常用來描述事物之間的關係。頂點用於代表事物（如人），連接兩頂點的邊則用於表示兩個事物間具有某種關係（如相互認識）。

考慮到現實社會存在大量節點（人口衆多），且這些節點之間存在錯綜複雜的聯繫（關係複雜），我們得到的這張複雜網絡就會出現簡單網絡所不具備的特殊拓撲特性。

從“大世界”到“小世界”——六度分隔理論

在日常生活中，一個常見的現象是，某些與你聊天的朋友也是你另一個朋友的朋友（禁止套娃）；某個你覺得完全無法結交的人，其實也是你朋友的朋友（禁止套娃+1）。人與人之間的關係往往會比你想象的更爲密切，所以社交網絡一般也被稱爲小世界網絡。

在網絡理論中，小世界網絡是一類特殊的複雜網絡結構，是一個由大量頂點構成的圖，其中任意兩個頂點之間的平均路徑長度比頂點數量小得多。換言之，雖然網絡中大部分的節點彼此並不相連，但絕大部分節點之間經過少數幾步就可到達。人類社交網絡就表現出明顯的小世界網絡特性。除此之外，互聯網、公共交通網、腦神經網等都有類似的特點。

（圖片來源：acfun）

小世界網絡的概念最早可以追溯到1929 年匈牙利著名作家考林西（Karinthy Frigyes）的短篇小說《鏈條》。小說中認爲人與人之間最多需要5層關係就可以建立起聯繫。1967年，哈佛大學社會心理學教授米爾格拉姆（Stanley Milgram）的連鎖信實驗，以及由此給出的“六度分隔”（six degrees of separation）假說（編者注：即最多通過六個人就能夠認識任何一個陌生人），開啓了學者對小世界網絡的學術探索。

考林西（左）與米爾格拉姆（右）

（圖片來源：wikipedia）

米爾格拉姆最初以美國堪薩斯州威奇托市爲起點，隨機選擇了60名志願者，他給了每位志願者一封信，並要求志願者將信傳遞給一位居住在馬薩諸塞州某指定地點的股票經紀人。早期的實驗雖然設計比較粗糙，但仍然有3封信送到了目的地。後經過多次改良實驗，米爾格拉姆成功將送達率提升至35%，後來更上升爲97%。

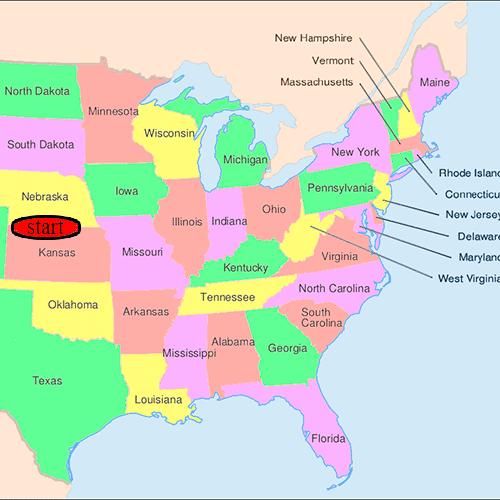
米爾格拉姆實驗中一條可能的傳遞路徑

（圖片來源：wikipedia）

不僅如此，米爾格拉姆還發現了所謂的漏斗效應，即大部分的傳遞都是由那些極少數的明星人物完成的。在一次樣本數爲160的實驗中，24封信最終送到收信人的家中，其中16封會經同一人送到；剩下的送到收信人辦公室的信件中，也有一半是由兩個人送來的。

這些實驗，爲後來小世界網絡的嚴格建模提供了支持。

小世界網絡的數學基礎

小世界網絡在社會學研究中被提出後，在相當長的時間裏都沒有與之相對應的數學模型。直到1998年，當時還在康奈爾大學攻讀博士學位的鄧肯·瓦茨（Duncan Watts）與導師斯蒂文·斯特羅加茨（Steven Strogatz）提出了一種新的複雜網絡模型，即著名的瓦茨-斯特羅加茨（WS）模型，這也是最經典的小世界網絡模型。

瓦茨（左）與斯特羅加茨（右）

鄧肯·瓦茨，賓夕法尼亞大學教授，曾任微軟紐約研究院首席研究員。斯蒂文·斯特羅加茨，康奈爾大學教授，同時也是一位科普作家。（圖片來源：wikipedia、stevenstrogatz.com）

WS模型首先定義了一個初始狀態（規則網絡），即每個節點都與一定距離的節點相連，也就是社交的初始狀態——首先與鄰居交朋友。假設節點數爲N（即研究對象總共有N個人），“鄰居”定義爲與此節點最近的2k個節點。此外，我們還要求k遠小於N。多言無益，直接上圖——

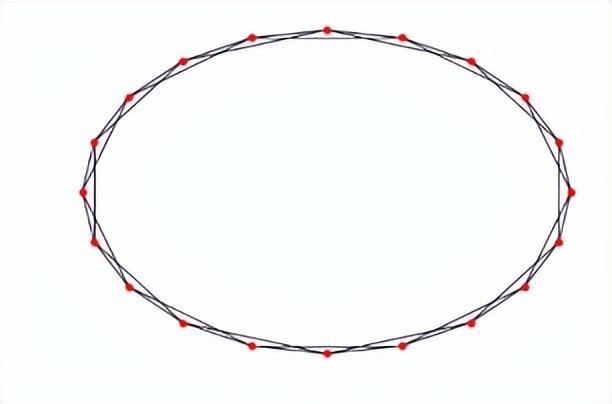
N=20（共有20個紅點），k=2（左右兩側各2個，共計4個"鄰居"），p=0（所有連接都不會被重連）

接下來，選擇規則網絡中的一個節點（標記爲1號），從它開始將所有節點順時針編號。然後1號節點的第1條連接會有0<p<1的概率被重連（保持與1號節點連接的一端不變，將另一端隨機換成網絡裏的另一個節點，但不能使得兩個節點之間有多於1個連接）。2，3，…，N號節點依次類推。然後再從1號節點的第2條連接開始，重複上面步驟。當所有節點的所有連接都經歷上面的步驟，操作結束，得到小世界網絡。

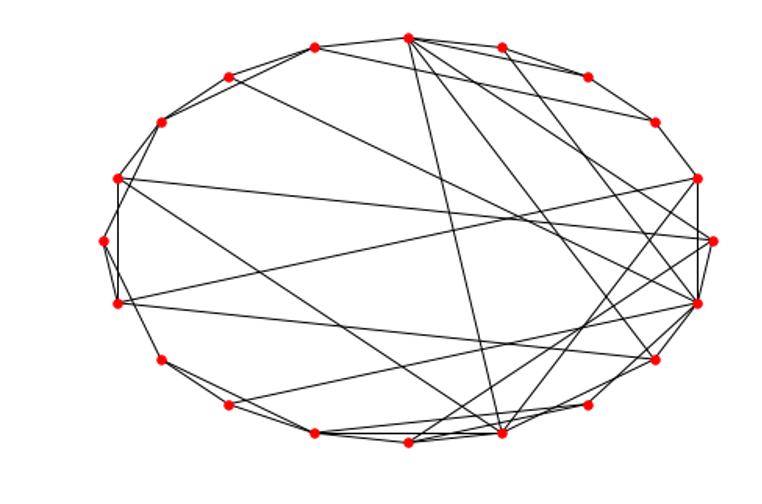
N=20，k=2，p=0.5（即每條連接有50%概率被重連）

當然我們也可以讓這個過程極端一些，譬如令p=1，我們將得到一張更爲混亂的圖，即隨機網絡。

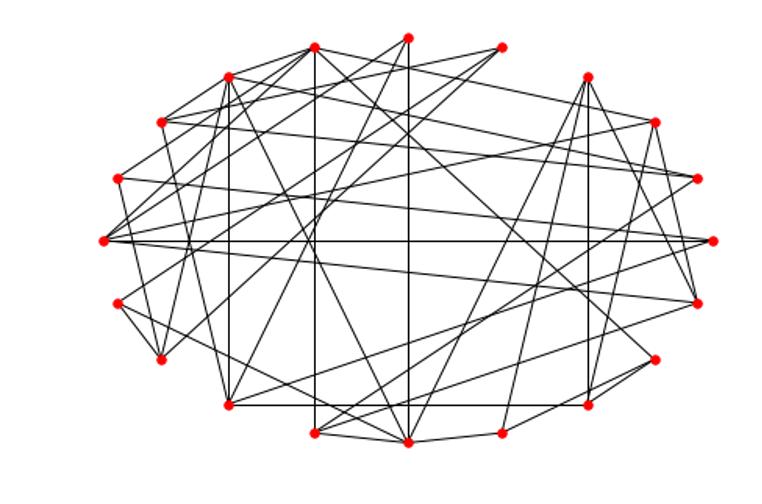
N=20，k=2，p=1（即每條連接都被重連）

“病因”大揭祕

有了上面的一系列鋪墊，讓我們最終步入正題，看看所謂的社交牛X症的發病原因，及其背後的數學原理。

首先讓我們考慮社交達人所具有的屬性。有人可能會覺得，“社牛”必定朋友多多。但根據英國人類學家羅賓·鄧巴的研究，一個人維持緊密人際關係的人數是有上限的，一般而言爲150左右。換言之，有些人雖然“認識”很多人，但不能建立更進一步的關係。所以相較於朋友的數量，朋友圈整體質量更能反映一個人“社牛”的程度。

敢於亂搭訕並不能證明你就是“社牛”，因爲——

（圖片來源：giphy.com）

所以在本研究中，我們沿用WS模型的設定，假設每個節點的鄰居都爲2k。同時定義“所有與某節點相連的點之間的實際邊數，除以這些點之間可能存在的邊數的最大值”爲集聚係數（編者注：可反映節點之間結集成團的程度）。爲了方便大家理解，把上面的定義寫成簡單的數學表達式：

沒看明白？點擊捋思路

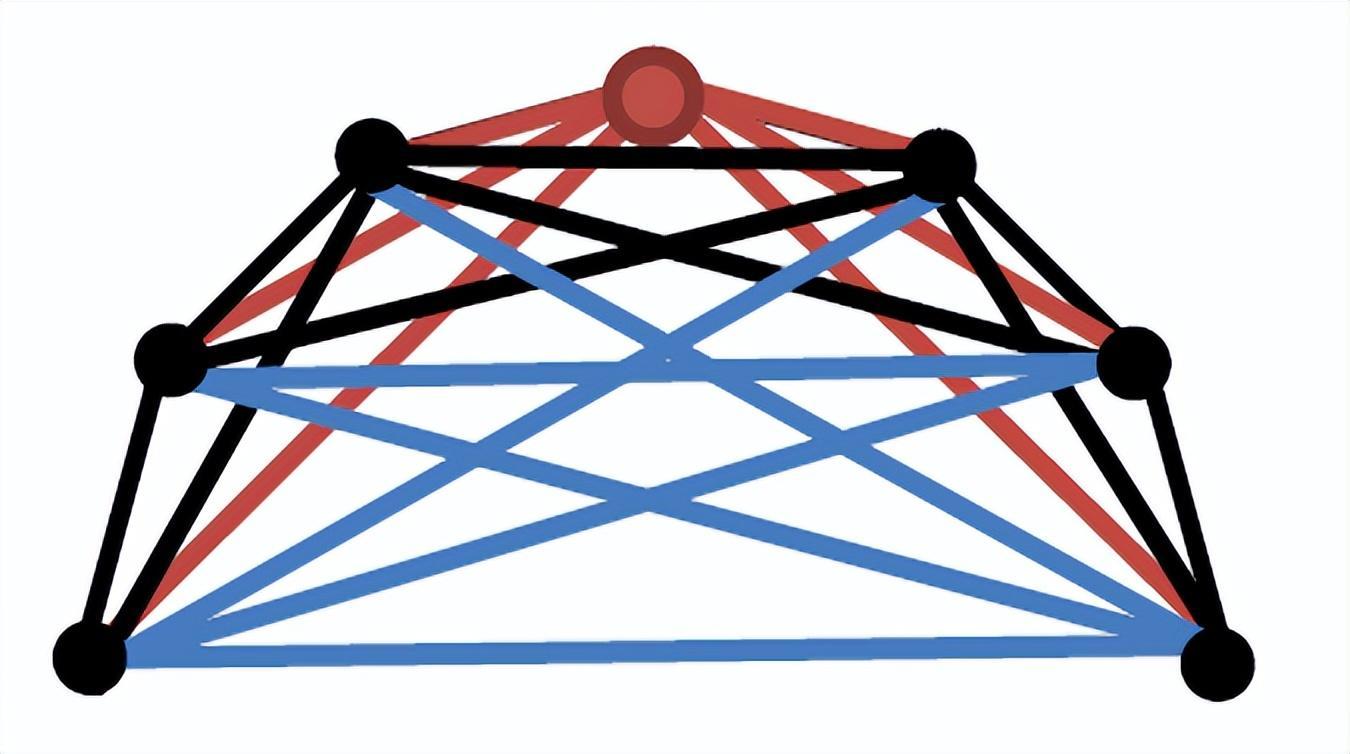
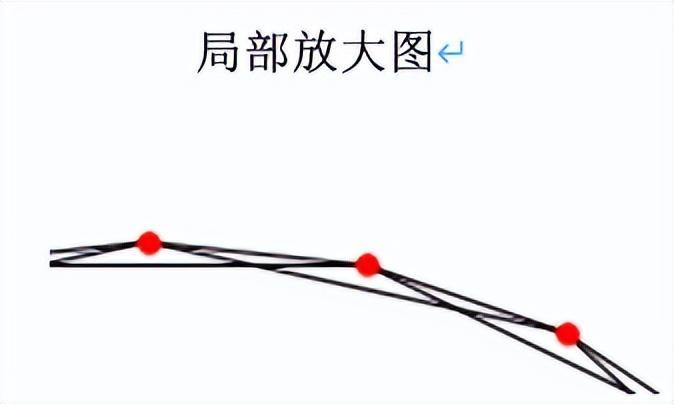
爲了方便理解，這裏再舉一個例子。取最簡單的情況，p=0，k=3，上圖中紅點定義爲點i，Cimax=藍色邊+黑色邊，Ni=黑色邊。

對於最簡單的情況，p=0（規則網絡），我們可以利用小學數學知識（這裏真的是小學數學——植樹問題的變種有木有），計算Ci。

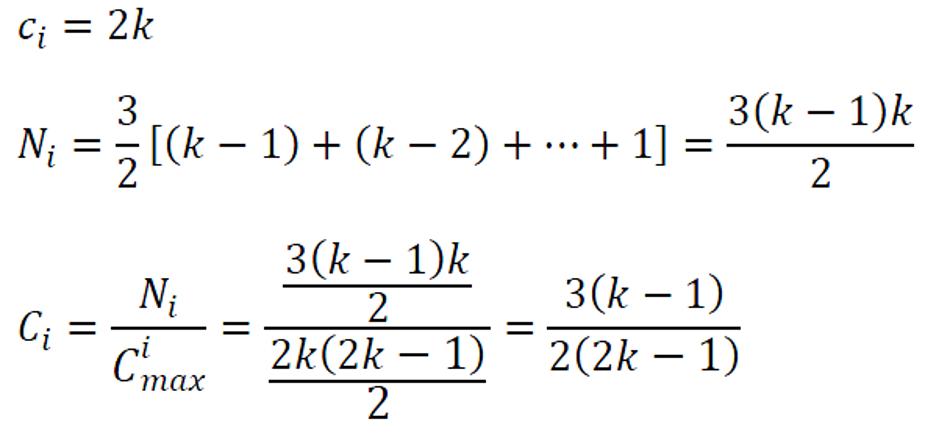
由於規則網絡中每個點的情況都是相同的，所以整個網絡中所有節點的集聚係數的平均值也等於上面得到的Ci。而對於一般情況，當p>0時，我們也可以求得每個點的集聚係數和整張網絡的平均集聚係數。根據Barrat和Weigt的數值模擬，網絡的平均集聚係數可以近似地記作：

類似地，我們可以定義節點間的路徑長度dij，進而求得整個網絡所有節點間的平均路徑長度L。平均路徑長度指示了網絡中兩點間最短距離的平均值。

值得一提的是，對於社交網絡（也就是圖論研究的圖）而言，存在有向圖（與節點相聯的邊有出入之分）和無向圖兩種情況。上面介紹的結論皆是以無向圖作爲研究對象，但有向圖的分析方法類似，只是需要區分dij與dji。

無向圖（“你愛我呀我愛你”）vs有向圖（“你不要過來啊”）（圖片來源：giphy.com）

綜上所述，當0<p<1時，集聚係數和平均路徑長度都可以視爲概率p的函數。根據瓦茨和斯特羅加茨的數值模擬及針對電影演員人際關係、電力網絡和秀麗隱杆線蟲（C.elegans）神經網絡的實證研究，p從0到1的過程中，平均路徑長度L下降很快，而集聚係數C下降較慢。

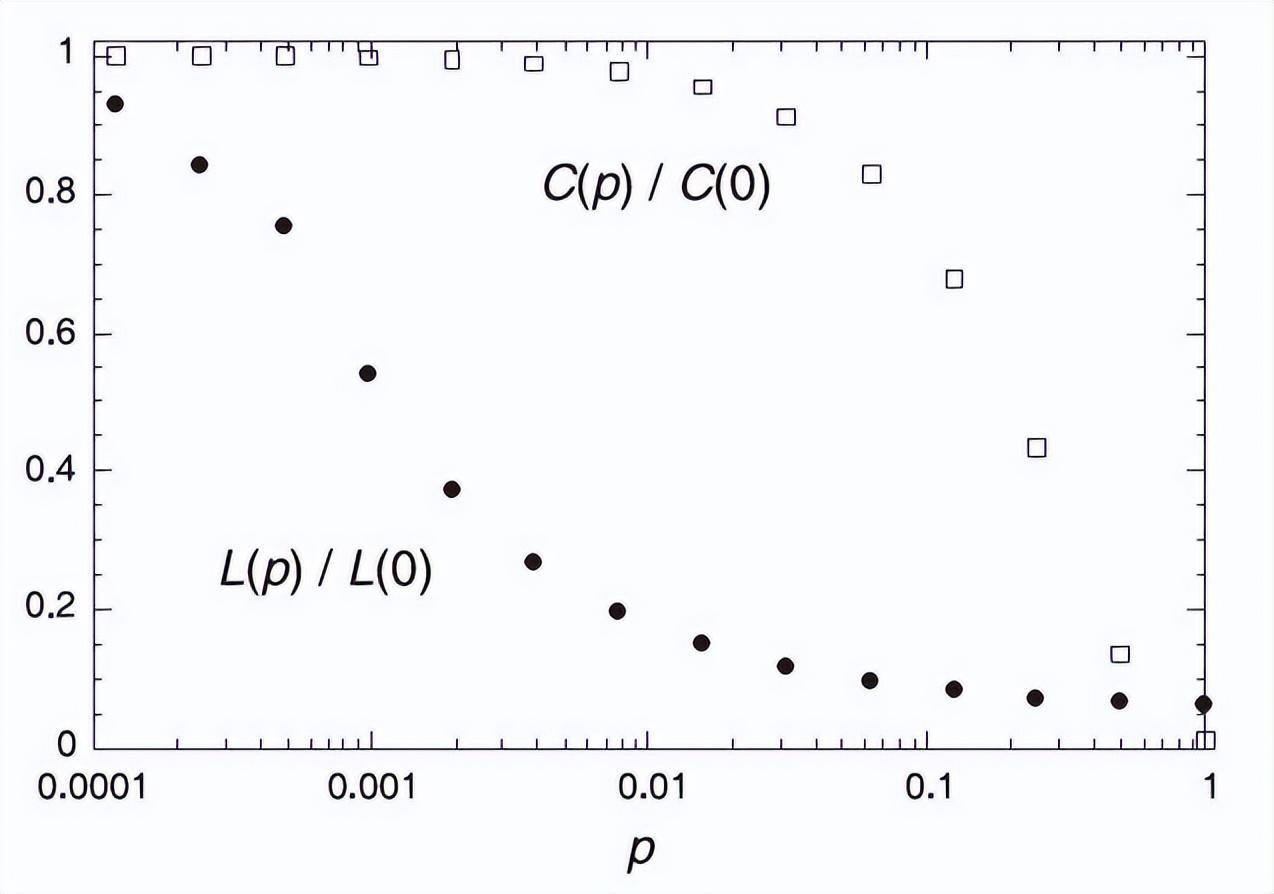
圖中橫軸的長度爲概率p的對數，縱軸是比值。實心點和空心點分別代表L(p)/L(0)與C(p)/C(0)。隨着p的增大，L(p)迅速下降；當p>0.1之後，C(p)纔開始顯著下降。這也是小世界網絡最顯著的特徵之一。（圖片來源：參考資料[6]）

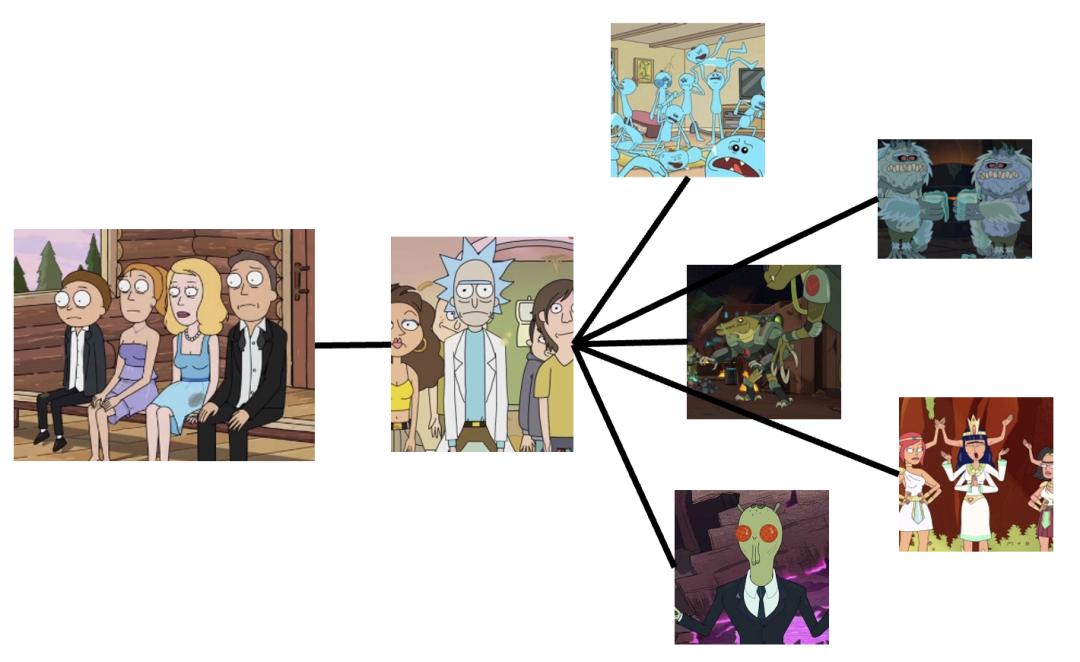
舉個例子，莫蒂一家本是普普通通的地球人，但是有了瑞克這個“社牛”患者，他們可以輕輕鬆鬆地與其他星球的生物建立鏈接，節點間的路徑長度大大減少，社交網絡的效率大大提高。

然而，如果人人都表現得“社牛”（如第二季第四集外星寄生蟲入侵後，整個屋子都是“熟人”），反而會使得集聚係數快速下降，“小團體”（譬如莫蒂原本的家庭）分崩離析。

小世界網絡模型說明，路徑重連會使得整個網絡的平均路徑長度迅速下降。換言之，少數“社牛”（網絡樞紐）的存在會導致整個網絡的鏈接效率大大提高；現代社會人渴望擴大社交圈的範圍，也反過來催生了“社牛”的出現。

不過，當p達到一定數值（>0.1）之後，集聚係數會顯著下降。換言之，“社牛”過多會降低網絡結團的程度，進而減少網絡中“小團體”的出現。所以，“社牛”雖牛，多了也亂套啊。

其實，甭管你是“社牛”還是“社恐”，最重要的是，大院er都希望你能收穫人類高質量友誼！

參考鏈接：

[1]戴一奇，胡冠章，陳衛. 圖論與代數結構[M]. 北京：清華大學出版社，1995.

[2]Blass, T. (2004). The Man Who Shocked the World: The Life and Legacy of Stanley Milgram. Basic Books.

[3]Milgram, S. (1967). "The Small World Problem". Psychology Today. Ziff-Davis Publishing Company.

[4]Travers, J., Milgram, S. (1969). "An Experimental Study of the Small World Problem". Sociometry. 32 (4): 425–443.

[5]Gladwell, Malcolm. "The Law of the Few". The Tipping Point. Little Brown. pp. 34–38.

[6]Watts D.J., Strogatz S.H. (1998). "Collective dynamics of ''small-world'' networks". Nature. 393 (6684): 440–442.

[7]Small World Model – Using Python Networkx.

https://www.geeksforgeeks.org/small-world-model-using-python-networkx

[8]Dunbar, R. I. M. (1992). "Neocortex size as a constraint on group size in primates". Journal of Human Evolution. 22 (6): 469–493.

[9]Gladwell, M. (2000). The Tipping Point – How Little Things Make a Big Difference. Little, Brown and Company.

[10]章忠志、榮莉莉、周濤 (2005), 一類無標度合作網絡的演化模型. 系統工程理論與實踐. 11: 55–60.

[11]Barrat, A., Weigt, M. (2000). "On the properties of small-world network models". European Physical Journal B. 13 (3): 547–560.

[12] 汪小帆,李翔,陳關榮. 複雜網絡理論及其應用[M]. 清華大學出版社，2006.

作者：鑄雪