自然界是人類創新靈感的不竭源泉。自然界生物具有非凡的適應能力和智慧：蟻羣如何找到距離食物源的最短路徑，大雁覓食時怎麼飛距離最短，生物怎麼進化出各種性狀……合理利用這些規律，可以處理……數學問題？

（圖片來源：veer圖庫）

沒錯，而且是處理傳統數學理論不易解決的問題。

優化問題與啓發式算法

首先，來看個數學問題：

計算如下一元二次函數的最值

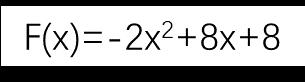
對這種簡單的目標函數，可直接套用公式：當自變量x=-b/2a時，目標函數的最值爲（4ac-b2）/4a（忘了請自行聯繫高中數學老師）。這種能直接表達爲公式的解，稱爲解析解（Analytic Solution）。

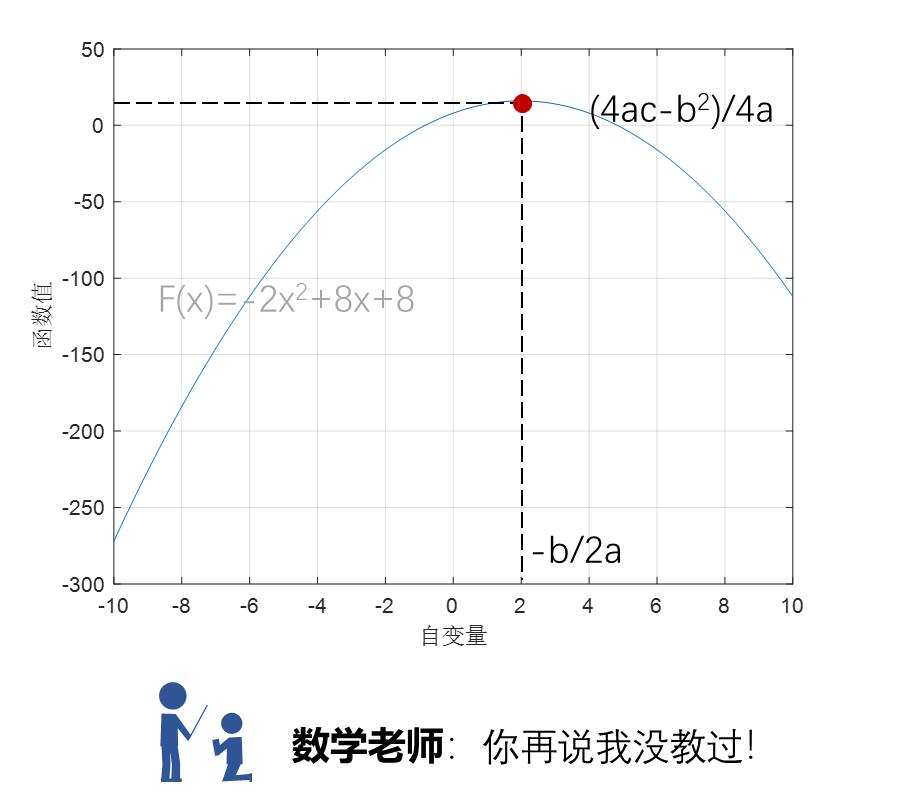
對於簡單問題，可一步得到答案

這種求某函數的最大值/最小值的問題，就是優化問題，這一函數稱爲目標函數（Objective Function）。優化算法，就是計算目標函數最值的算法。

實際中，優化問題的目標函數往往比較複雜，無法得到解析解，因此常利用梯度（多元函數的導數），進行迭代求解。

然而，對於某些更爲複雜的目標函數，無法使用梯度方法。例如，計算如下函數的最小值

複雜的目標函數，無法套用公式

若利用常規的梯度方法，容易收斂於局部最優（Local Optimum），即某一範圍內的最值點，而不是全局最優（Global Optimum），即全局範圍內的最值點。

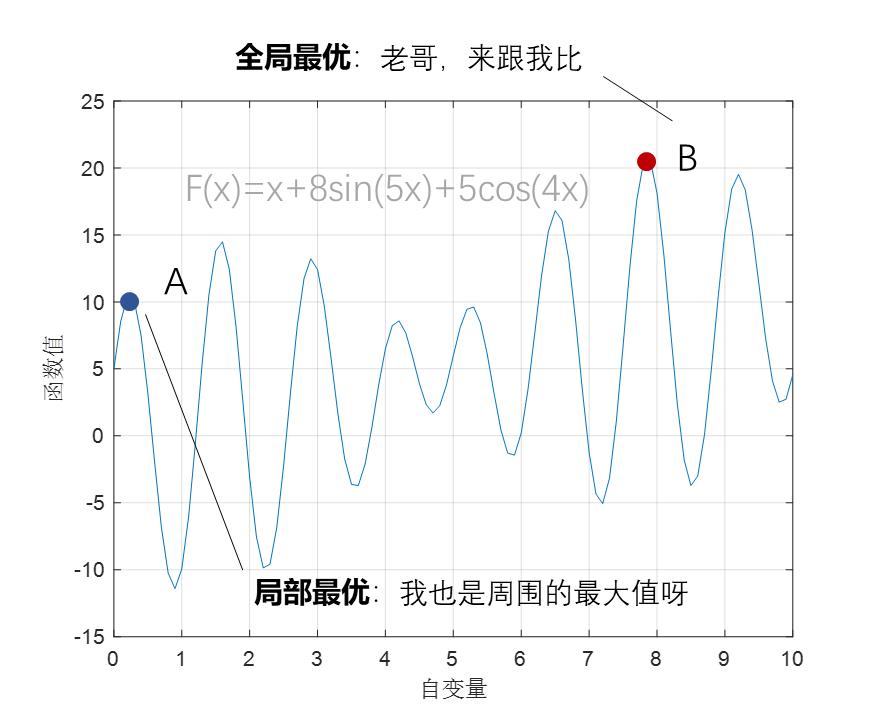
梯度方法容易陷入局部最優

優化類似的複雜函數，一直是難點問題。科學家在受到某些自然規律的啓發後，模擬自然體算法，提出了若干啓發式算法（Heuristic Algorithm），用於處理傳統數學理論不易解決的優化問題。

例如，模擬蟻羣尋找、搬運食物的規律，提出蟻羣算法（Ant Colony Algorithm）；模擬大雁在空中覓食的規律，提出粒子羣優化算法（Particle Swarm Optimization Algorithm）；模擬生物遺傳與進化規律，提出遺傳算法（Genetic Algorithm）……

算法科學家怎麼看生物遺傳與進化？

本文介紹的啓發式算法，是模擬生物遺傳與進化規律提出的，那麼，算法科學家眼中的遺傳與進化是怎樣的？這裏先以長頸鹿的進化爲例（注意，遺傳算法只是對已知進化規律的模仿，並不一定等同於生物規律）。

自然界的生物多種多樣，其性狀由基因和外部因素共同決定，但基因佔主導作用，因此這裏忽略外部因素。例如，基因確定，長頸鹿的脖子長短也隨之確定。

基因是生物的遺傳物質，由多位核苷酸組成，類似於“AaBbCc”。種羣的進化，必然意味着基因的變化。

自然選擇並不直接作用於基因，而是作用於性狀。個體的性狀不同，其生存能力不同。例如，鹿脖子越長，喫到的樹葉越多，生存能力越強。將生存能力進行量化，稱爲適應度。

適應度本應由多個因素共同決定，例如鹿的脖子長短、體力、視力等因素。但這裏僅考慮脖子長短，脖子越長，適應度越高。

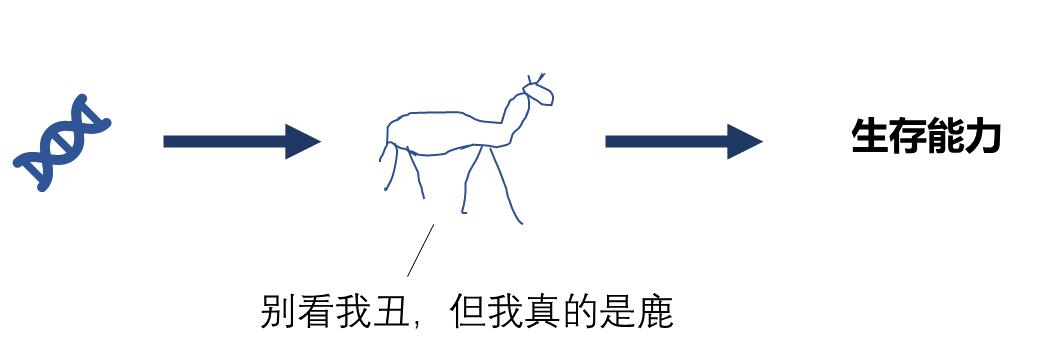
（本文默認：基因決定性狀，再決定生存能力）

從前，有羣普通的鹿，大家的基因各不相同，因此性狀也不同（這裏的性狀特指脖子長短），將這一代的鹿羣記爲“鹿羣0”。

在“鹿羣0”中，脖子長的個體能喫到更多的樹葉，更可能生存下去，因此適應度高。而脖子短的個體更可能被淘汰，適應度低。將這一過程稱爲選擇，經過選擇生存下來的鹿才能夠進行交配。

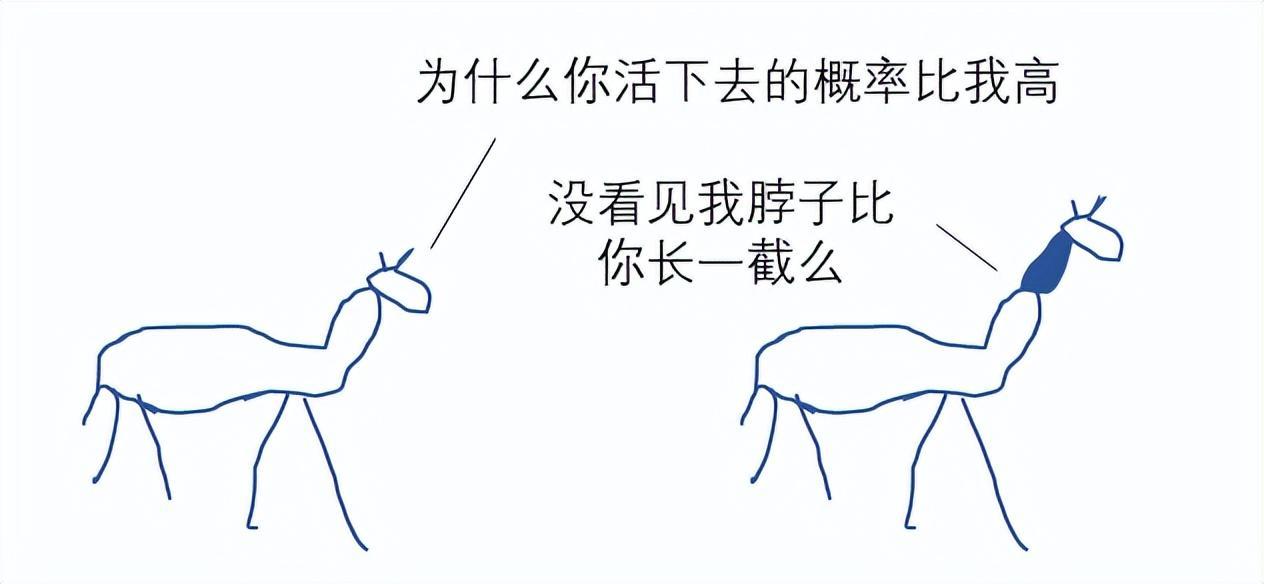
（圖片來源：望墨溢，一位靈魂畫家）

雄鹿在與雌鹿交配時，不是簡單地複製自己的基因，而是與雌鹿的基因發生交叉後再結合（這裏認爲基因=染色體）。例如，“Aa BbCc”+“aa bbcc”=“Aa bbcc”+“aa BbCc”。

當然，在兩條基因進行結合時，基因的一位或若干位核苷酸可能發生變異。例如，某位基因b變異成B。

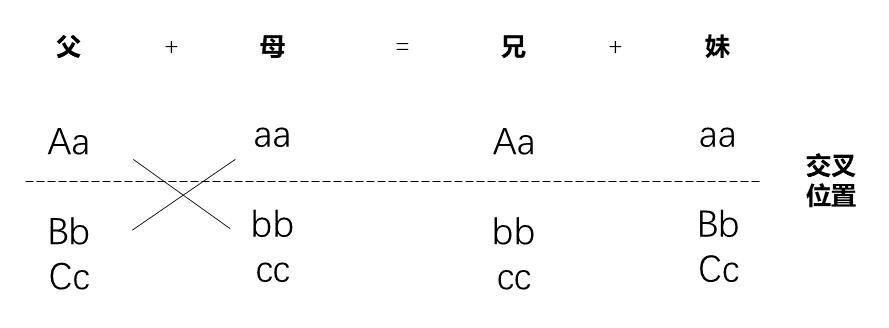
基因交叉

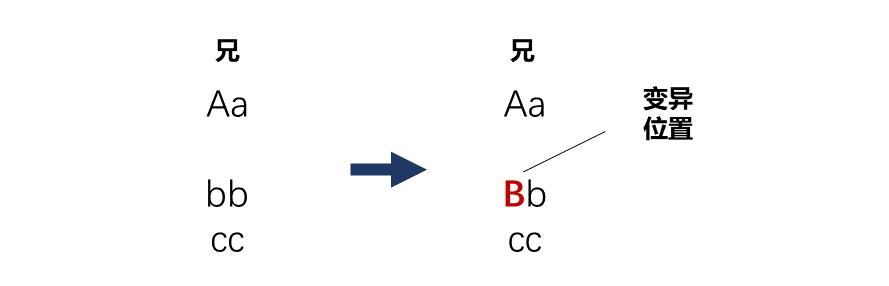
基因變異

這樣，“鹿羣0”就產生了新的一代，記爲“鹿羣1”。一般而言，經過選擇處理的“鹿羣1”，適應度的最大值和平均值會提高，也就是脖子長短的最大值和平均值有所提高。

經過一代又一代的繁衍，由於基因的變化，“鹿羣N”的脖子將會顯著長於“鹿羣0”，適應度更高。這時，我們可以說物種進化了。

種羣趨向最優

當然，最優的脖子長短還與環境有關，這裏環境特指樹冠高度。脖子高於樹冠，沒有好處反而有壞處。而只要環境不發生顯著變化，“鹿羣N”之後，種羣的基因不會發生顯著變化，適應度也不會發生顯著變化，種羣穩定在最優解。

遺傳算法，到底怎麼算？

美國的John Holland，模擬達爾文生物進化論的自然選擇和遺傳學機理，提出一種啓發式優化算法——遺傳算法。

該算法將自變量轉換成個體，通過編碼將個體與基因對應起來，將待求解的目標函數作爲適應度函數，保留了交叉、變異，經多次迭代後，可使種羣（多個個體）趨於最優解。

以求解目標函數F(x)=x+8sin(5x)+5cos(4x)的最大值爲例，遺傳算法會分六步走來解決問題：

1. 初始化

遺傳算法將自變量可能的取值視爲個體，在設置好種羣總數後，生成初始化種羣。例如，設置種羣個體共100個，在[0,8]區間內隨機選擇100個初始值。

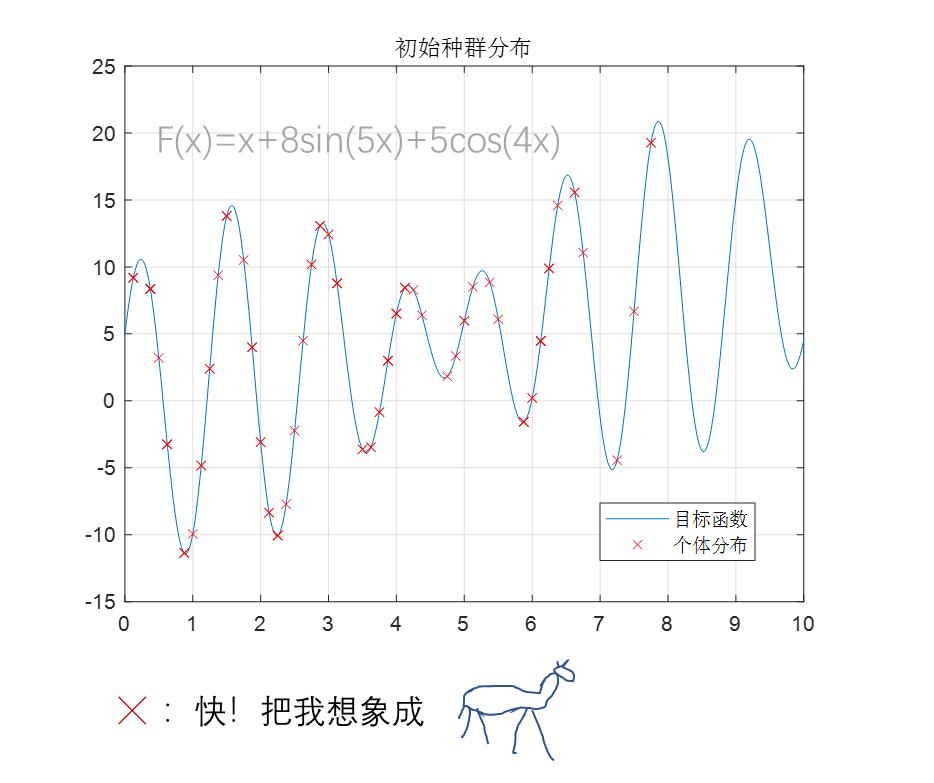
在自變量的某個區間內，隨機生成初始種羣

2. 編碼與解碼

自變量個體本身無法視爲基因，需將其進行某種轉換，通常將個體轉換爲一串二進制的數，稱爲編碼，這串二進制的數即可視爲基因。

例如，規定用4位二進制表示整數部分，用2位二進制表示小數部分，則3.25可表示爲“001101”，“001101”就是該個體的基因。

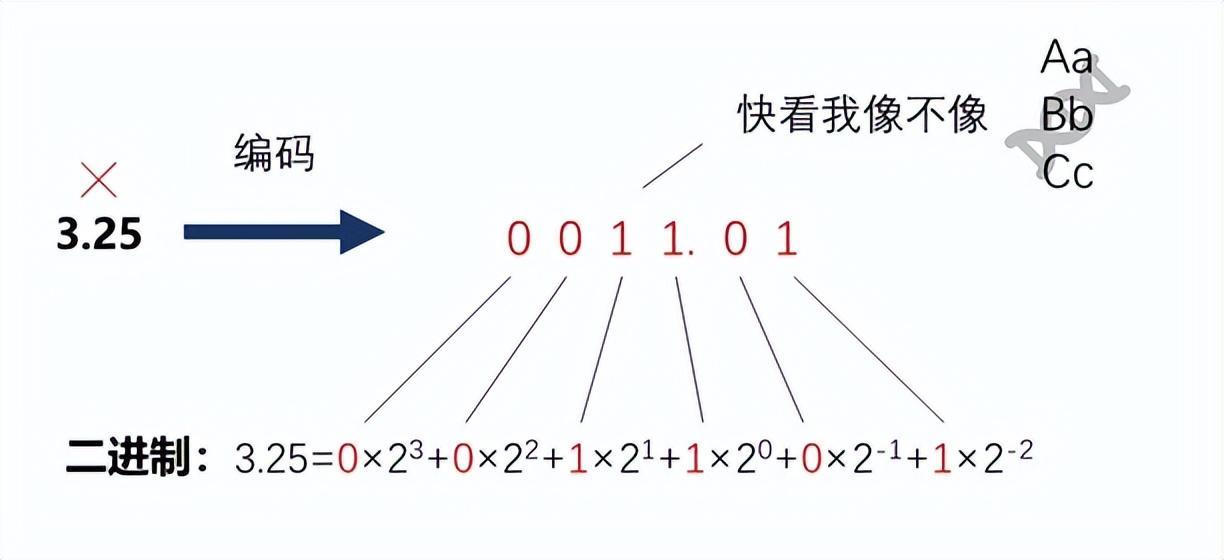
個體的3.25的二進制表示001101，就是對基因的模擬

編碼是爲了模擬基因，從而進行後續的交叉、變異。而解碼，就是將基因（二進制）再轉換爲個體（十進制）。十進制數才能代入適應度函數中，從而計算適應度。

3. 適應度計算

但在將基因（二進制）轉化爲個體（十進制）後，將十進制個體代入目標函數，即可得到適應度。

不難理解，適應度函數常常就是待求解的目標函數F(x)=x+8sin(5x)+5cos(4x)。

4. 選擇

每個個體，根據適應度大小，進行選擇。適應度大的，更可能被保留下來，適應度小的，更可能被淘汰。這一過程，通常用“輪盤賭”模型進行。

當然，在選擇的過程中，我們還得保證個體數量不變。爲保證這一點，適應度大的，不僅被保留，還會被複制。

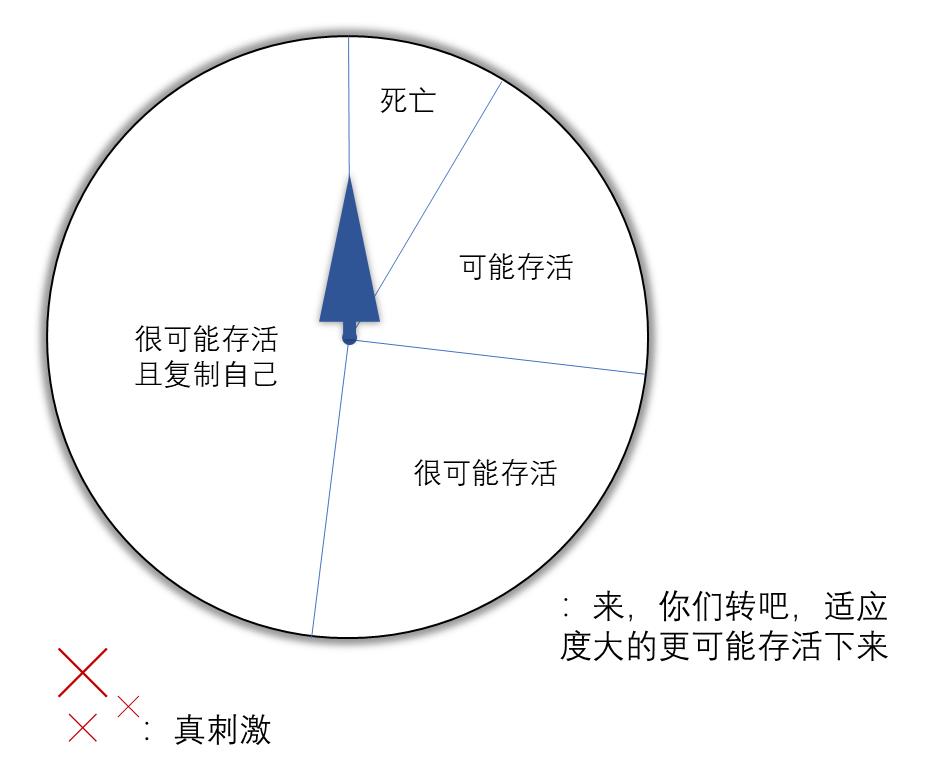
適應度大的個體自然更可能存活

5. 交叉與變異

保留下來個體，經編碼得到基因後，進行交叉。例如，“001 101”+“010 010”=“001 010”+“010 101”。一般而言，交叉點是隨機選擇的。

這裏，兩個基因交叉得到兩個新的基因（相當於父母必生雙胞胎）。因此，交叉不改變種羣數量。

在交叉後，每個基因還可能發生變異。一般而言，變異點也是隨機的。例如，某位的1變爲0，或0變爲1。

二進制數的交叉

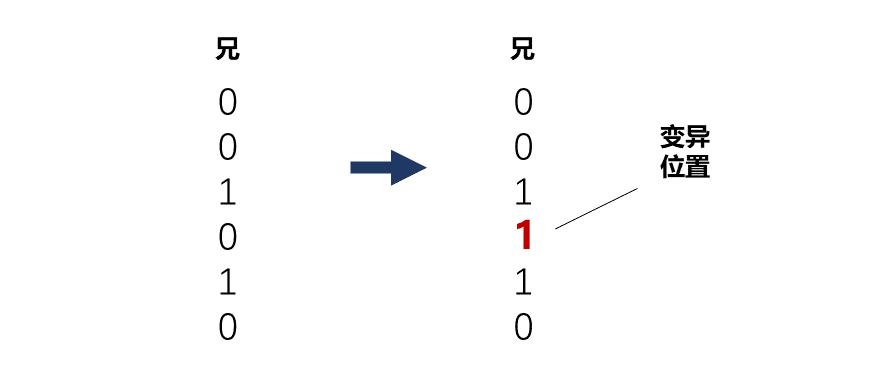
二進制數的變異

在經過選擇後，相比前一代，種羣適應度的最大值和平均值都會有所提高。具體而言，就是所有的個體都會向目標函數的高處集中。經多次迭代後，就會集中於最大值處。

6. 是否結束

既然是優化算法，必然需要設置結束條件，不能讓算法無限次地循環下去（死循環）。最簡單的方法，就是設置算法運行次數。例如，令算法循環50次後結束。

這裏給出遺傳算法一般的流程圖

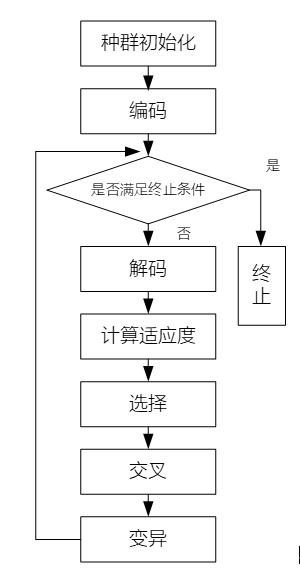
隨着進化的進行，即算法的循環，種羣的平均適應度勢必逐代提高，最終收斂於某一最大值，這一點就是我們要找的目標函數的最大值點。

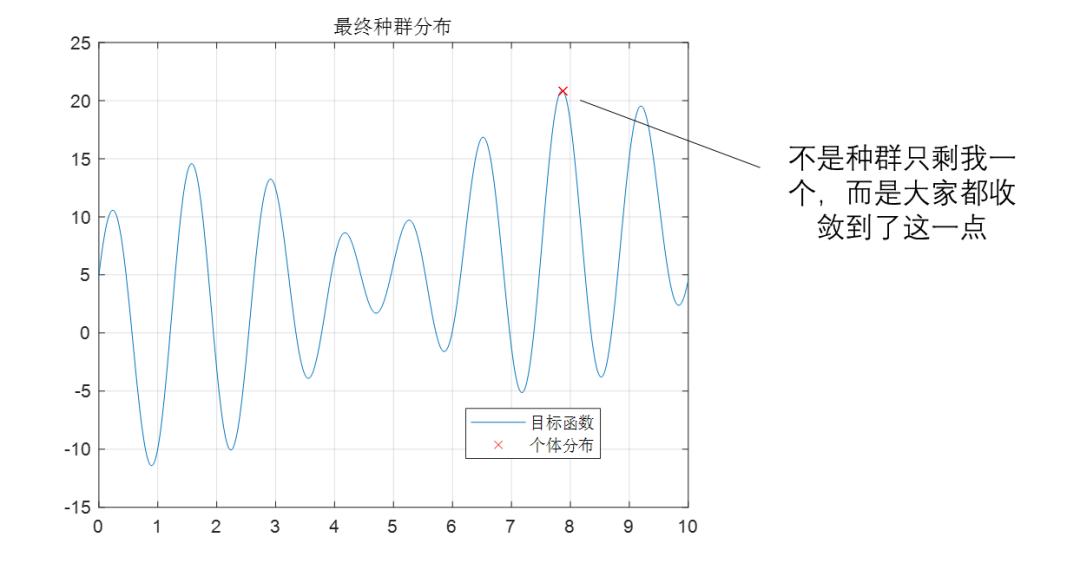
遺傳算法循環50次後的種羣分佈：集中於一點

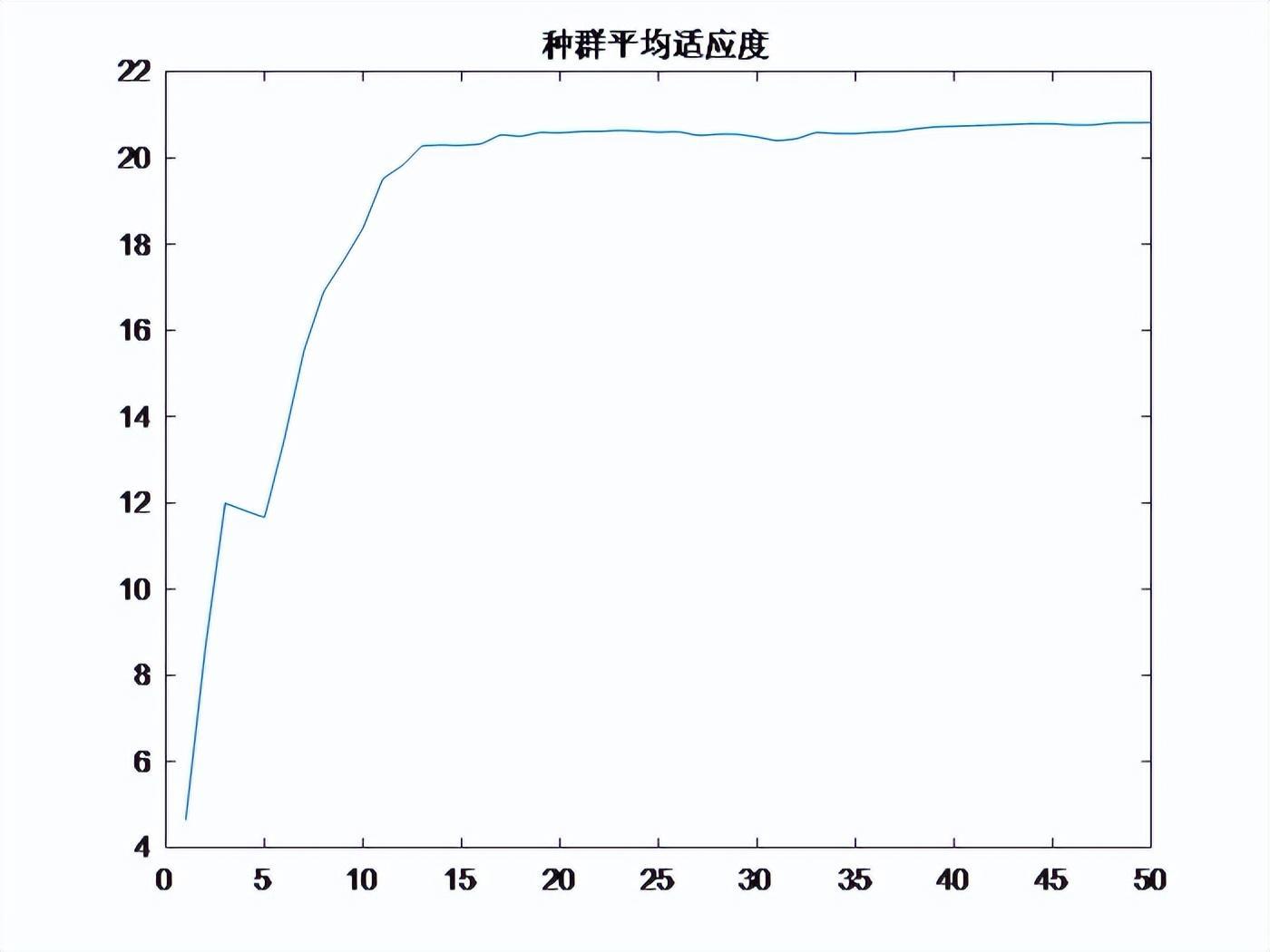
隨着算法的迭代，種羣的平均適應度也在提高

每一步都有小策略

要想提高遺傳算法的效率，在上述步驟中其實都有小技巧。

1.初始化

若可獲得關於最值點的先驗信息，即最值點所在的大致範圍。則可在這一範圍內生成初始種羣。若沒有，則需要在更大範圍內隨機生成。

初始值的選擇，會影響算法的收斂速度。初始值選得越靠近最優解，收斂速度越快。另外，不合適的初始值，可能使得算法陷入局部最優。

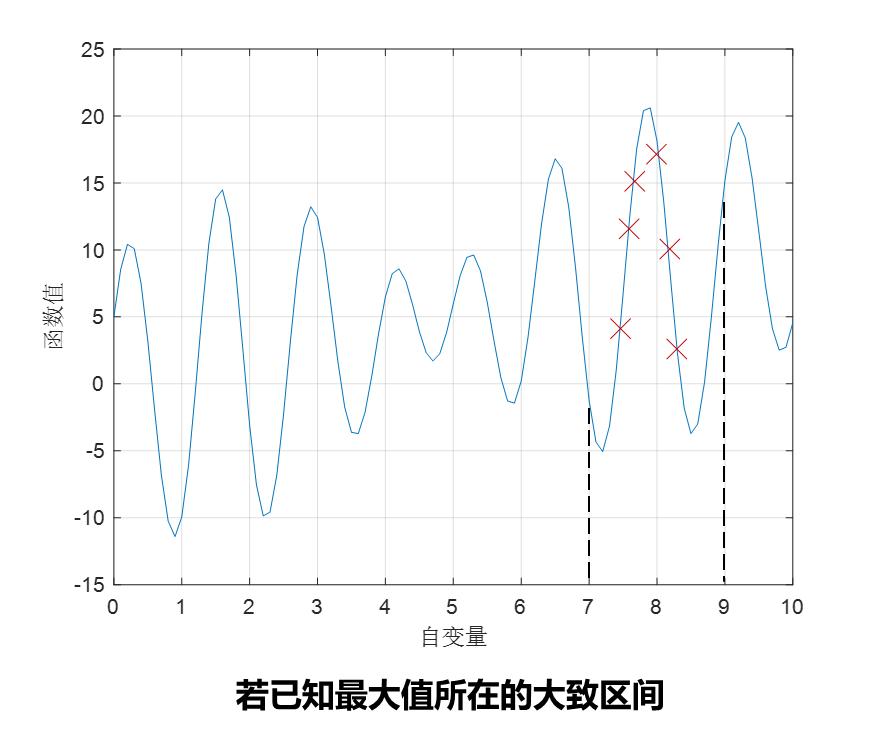
這樣是不是能更快地找到最優解~

2. 編碼與解碼

在數字信號處理中，度量必然存在最小值和最大值，即變量的取值不是連續、無限的，而是不連續，有限的，由於度量產生的誤差稱爲量化誤差（Quantization Error）。

例如，我們用4位二進制表示整數部分，用2位二進制表示小數部分，那麼自變量最大隻能取15.75（對應二進制爲111111），且小數部分只能分辨出0.25的差異。度量的最小值又被稱爲分辨率（Resolution Ratio）。

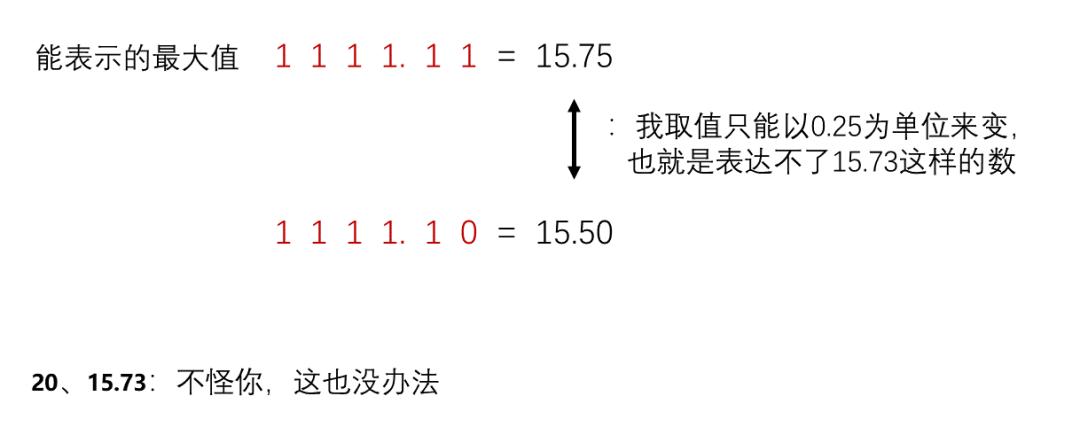
F(x)=x+8sin(5x)+5cos(4x)的最優解在7.860處，但算法只能收斂於7.875

當然，我們可令基因的長度很長，例如用100位二進制表示整數部分，10位二進制表示小數部分，即可擴大自變量取值範圍，提升分辨率。然而，這樣會增加算法的運算量和存儲量。

3. 選擇

在選擇過程中，若一定保留、複製適應度最高的個體，則稱爲精英保留（Elite Reservation）；若不一定保留適應度最高的個體，其依舊有可能被淘汰，則稱無精英保留。

實驗證明，有精英保留的遺傳算法，收斂至最優值的速度更快，且更爲穩定。

4. 交叉與變異

交叉可分爲單點交叉，也可多點交叉，變異也可分爲單點變異和多點變異。交叉和變異是爲了提高基因多樣性，加速收斂速度，且可跳出局部最優。

例如，當所有個體都集中至局部最優附近時，突然有個個體變異了，“跳”至全局最優附件，則種羣就可進一步進化。

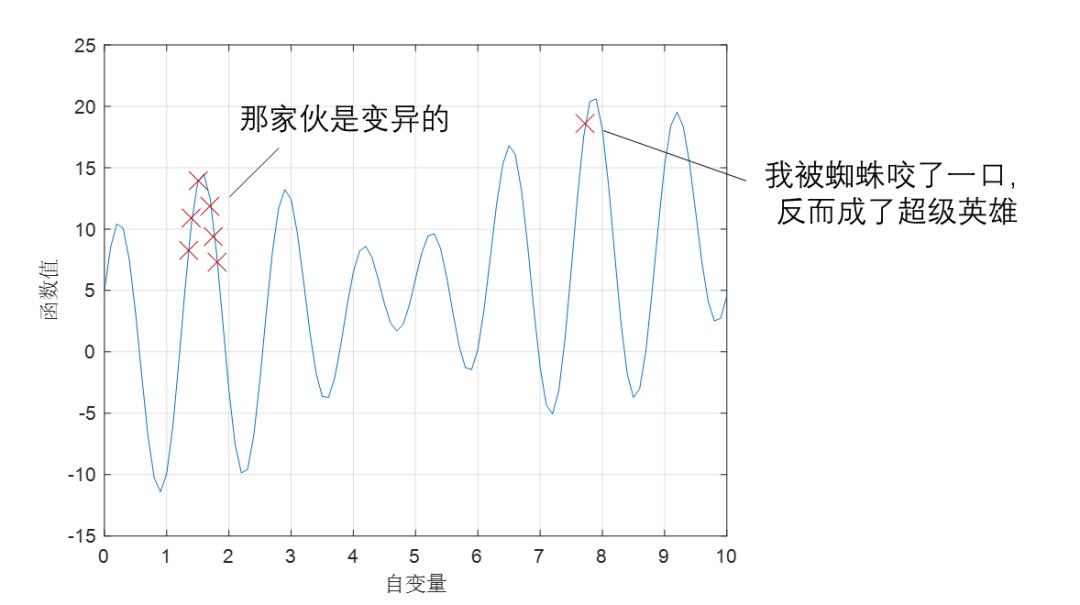
對於種羣而言，穩定比多樣更爲重要，因此交叉和變異往往單點進行即可，且變異概率往往非常低。

5. 是否結束

通過設置算法運行次數，來控制算法結束，雖然簡便，但存在如下兩個問題：

（1）若算法收斂較慢，例如50次並未使得種羣集中到某一最優解，那麼結果必然不正確；

（2）若算法收斂較快，例如20次即可使得種羣集中到某一最優解，那麼就浪費了很多的計算資源。

另一種更爲可靠的方法，是判斷相鄰2次運算間，種羣的平均適應度差異大小，即是否小於某個門限。如果是，則認爲算法已經收斂，可終止；如果否，則認爲算法還未收斂，應繼續循環。

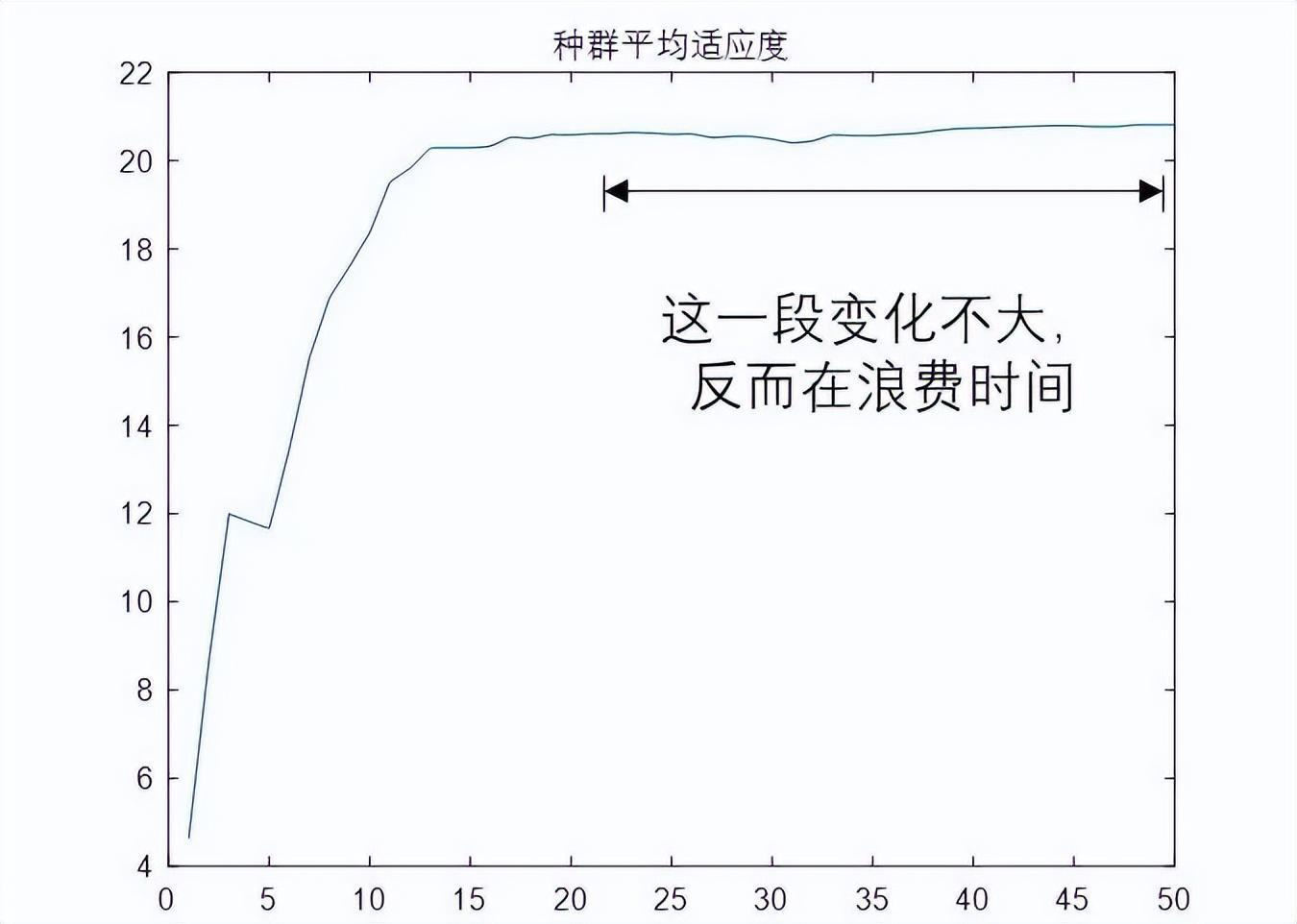
根據平均適應度差異來控制算法終止，更爲可靠

遺傳算法不僅能畫畫，還能告訴你這些

以遺傳算法爲例的啓發式算法，沒有極其嚴格的數學推導，但自然界已用這些規律解決了無數的問題。現在，遺傳算法已廣泛應用於我們生活中的多個領域，例如，如何設計車輛外形，以減少空氣阻力；如何安排機器人的工作流程，以提高工作效率；如何進行線路規劃，使快遞運輸路程最短……

去年，有人在GitHub上傳了一個項目，就是用遺傳算法來繪製特定的圖片，下面是一個仿真實例，看遺傳算法是如何對照上面的照片“畫”出下面的作品的：

（圖片來源：https://github.com/anopara/genetic-drawing）

首先，給出多個初始色條，組成色條畫面，並以色條畫面與原圖片的差作爲目標函數。然後利用遺傳算法，迭代求解色條的排列，使得目標函數最小，即色條畫面與原圖片“最像”，從而實現用多個色條“畫”出原圖片。

PS：如果你不是碼農，暫時也不需要用到遺傳算法，但是仍可從遺傳算法中學到若干智慧：

●沒有完美的算法，保證精度，就得增加計算量。一切策略，都是在多個因素間尋找平衡的藝術。

●只追求穩定，會無法進步；只追求多樣，會無法積累優勢。因此，我們需要在穩定和多樣間尋找平衡。但是，從長遠來看，穩定（積累、傳承）往往比多樣更重要一些。

●精英保留很重要，但也絕不能輕視精英以外的普通個體。沒有普通個體，變異就失去了土壤，種羣也就走向了單調。而單調，往往意味着脆弱。

參考文獻：

[1] 鄭樹泉. 工業智能技術與應用[M]. 上海: 上海科學技術出版社.

[2] 李德毅, 於劍. 中國科協新一代信息技術系列叢書 人工智能導論[M]. 北京: 中國科學技術出版社.

作者：望墨溢

作者單位：西北工業大學 航海學院

（本文於2021年7月26日首發於科學大院）